目次
はじめに
それでは、速度に関する3つの内容を見ていきます。
□動画による解説はこちら↓↓↓
平均の速度と瞬間の速度
まずは平均の速度と瞬間の速度です。

一般に、運動する物体は常に一定の速度で動いているわけではなく、時間と共に絶えず変化しています。
ある時刻の速さを瞬間の速度といい、特定の区間を進んだ時間と変位から求めた速度を平均の速度と言います。
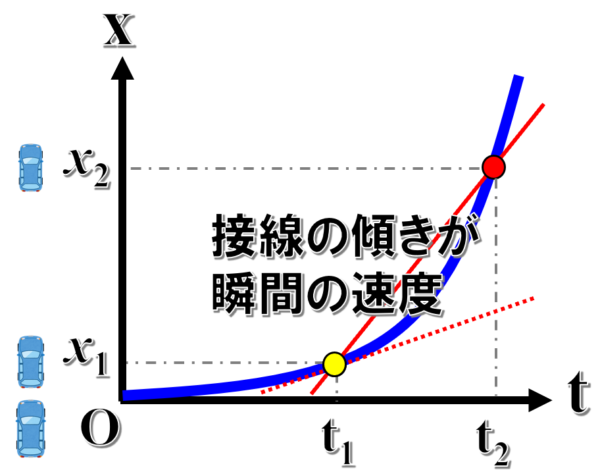
こちらのx-t図は、横軸に時間をとり、原点から出発したある物体の位置を縦軸とした時のグラフになります。
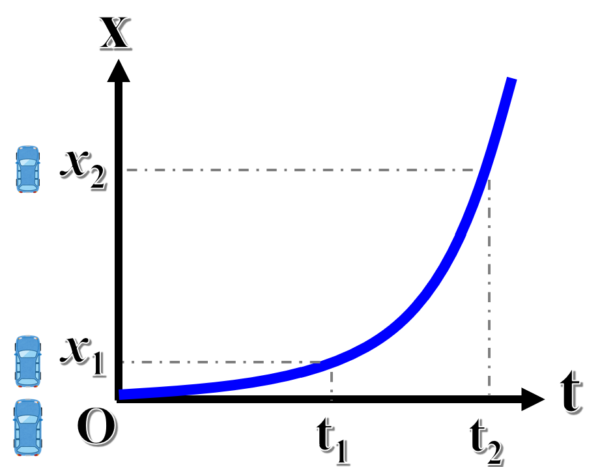
このグラフの曲線は、時間が経過するにつれて、物体の位置が大きく変化していることが読みとれます。

平均の速度は、特定の2点間の位置の変化量と所要時間から求められます。
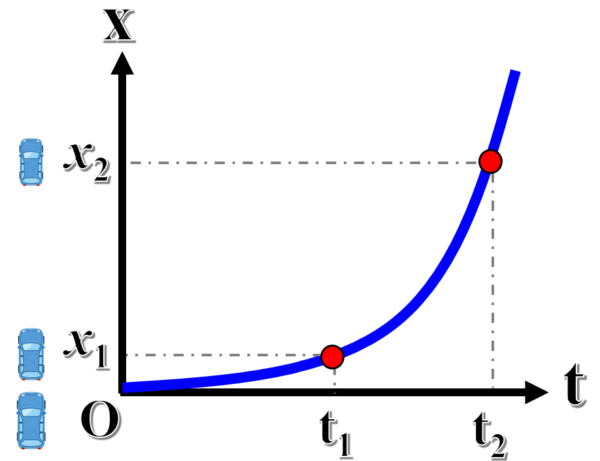

点Pの位置がx1、点Qの位置がx2だった時に、平均の速度は次の式で求めることが出来ます。

※vの上に付いている横線は、「バー」と読み、その値の平均値を表します。

この式は、x-tグラフ上では、2点間を結ぶグラフの傾きに一致しています。
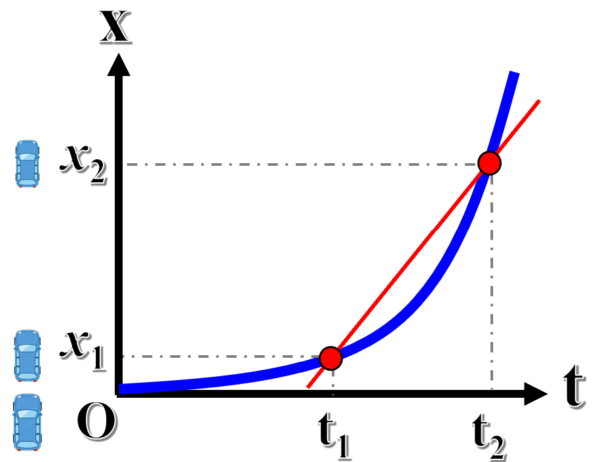
平均の速度は、Δという記号をつかって、
x2-x1=Δx
t2-t1 =Δt
と表して、Δt分のΔxという式で書くことが出来ます。

Δとは変化量を表す記号で、特定の2点間の差を取ることを意味した記号です。

また、Δxや、Δtの区間をゼロに近いくらい限りなく狭めていった時に、dx、dtと表現することがあります。


こちらもデルタx、デルタtと読みますが、こちらのデルタは、限りなくゼロに近い、微小時間であったり微小な距離という意味合いを含みます。
したがって、

と表記される速度は、ある瞬間の速度という意味となり、グラフ上では接線に点Pでの接線になります。
ある時刻における瞬間の速度は、x-tグラフ上で、その時刻の点に引いた接線の傾きとして表されます。
例題解説
ここで1つ問題を解いてみます。
図は、x軸上を運動する物体の位置x[m]と経過時間t[s]の関係を表している。図の直線aは、点Pにおける接線である。
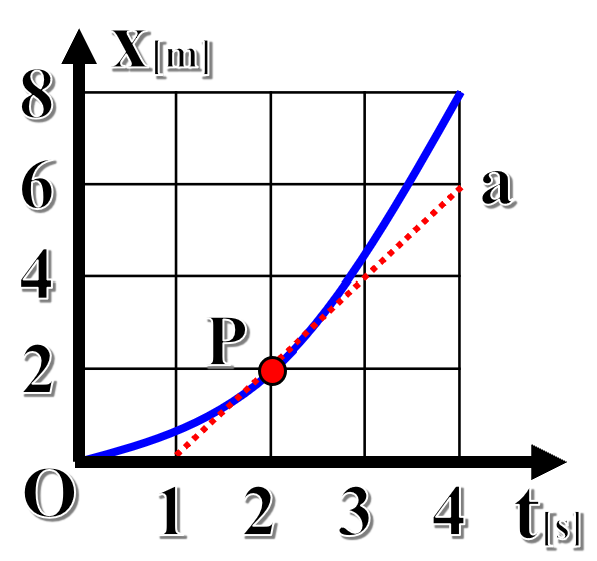
(1)時刻2.0~4.0秒の間の平均の速度vは何m/sか。
グラフより、物体は2.0秒の時は、2.0[m]の位置に、4.0秒の時には、8.0[m]の位置にいることが読み取れます。したがって、2.0秒から4.0秒までの2秒間に、8.0-2.0で差し引き6.0m移動したことになります。
これより、平均の速度を求めると、次のようになります。
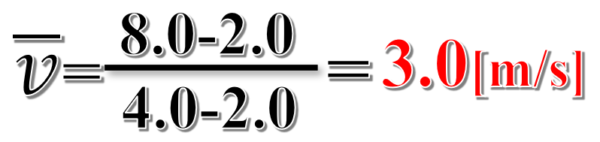
(2)時刻2.0秒における瞬間の速度vは何m/sか。
瞬間の速度は、x-tグラフ上では、その時刻の点に引いた接線の傾きとして表されます。
グラフより接線の傾きを求めると、t=1の時に、x=0、t=2の時に、x=2と読み取れます。
したがって、接線の傾きを求めると次のようになります。
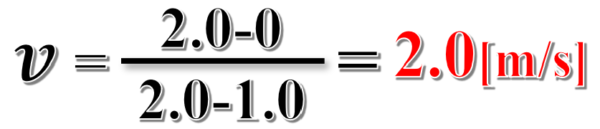
これが瞬間の速度になります。
速度の合成
次に、速度の合成に進んでいきます。

図は、川の中を一定の速度で進む船を示しています。船の速度は一定ですが、川の流れる方向によって、川岸で見ている人には、船の速度が早く見えたり遅く見えたりすることがあります。
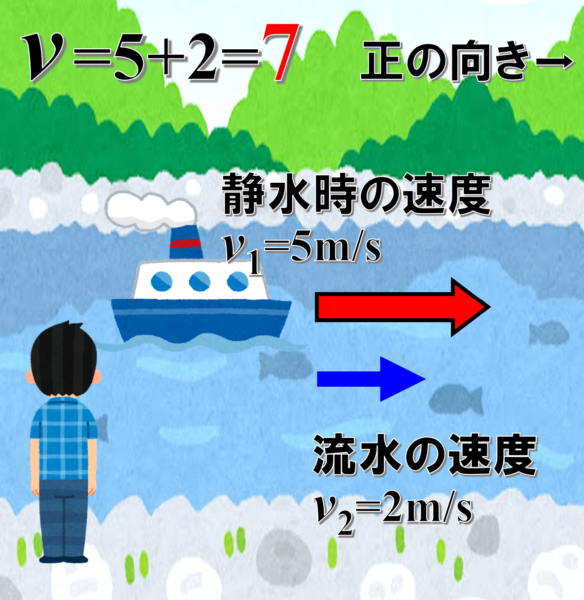
船の速度が右向きに5m/sだった時
同じ向きに川が流れている時、流水の速度が2m/sだったとすると、川岸で見ている人にとっては、5+2=7m/sで進んでいるように見えます。
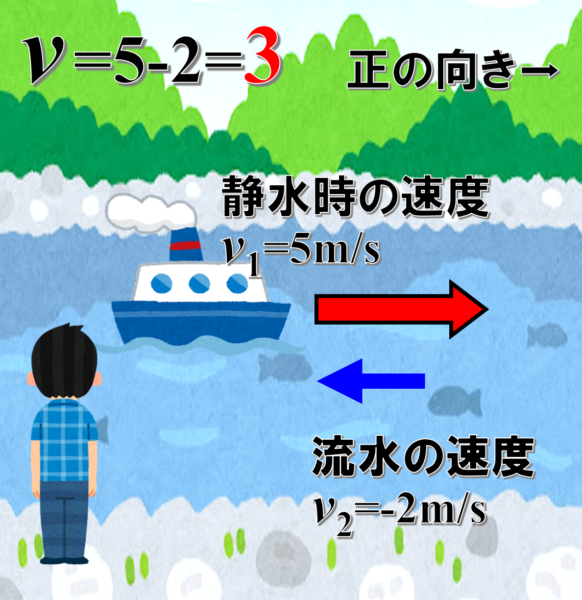
川の流れが逆向きになっている場合は、川岸で見ている人にとっては、5-2=3m/sで進んでいるように見えます。
一般に水の流れがない時の船の速度をv1とし、流水の速度をv2とすると、川岸で静止している人から見た船の速度vは次のように表されます。
![]()

相対速度
最後に相対速度です。
今まで物体の速度を見てきましたが、そこでは静止した状態から動く物体を見ていました。

しかし、同じ速度で動いている物体であっても、観測する人が動いている場合は、物体が早く見えたり遅く見えたりします。
例えば、時速40kmで走るバスの後ろを、時速30kmで走っているバイクから追いかけている人には、バスは時速10kmで遠ざかっていくように見えます。

一方、時速30kmで走るバスの後ろを、時速30kmで走っている場合は、バスとの位置関係が変わらないので、バスがあたかも静止しているように見えます。
![]()
また、時速20kmで走るバスの後ろを、時速30kmで走っている場合は、時速10kmで近づいてくるように見えます。
![]()

一般に動く物体Aから観測した他の物体Bの速度のことをAに対するBの相対速度といいます。
相対速度は、物体(相手)の速度から観測者の速度を引くことによって得られます。
物体A速度をvA、物体Bの速度をvB、物体Aから見た物体Bの相対速度をvABとすると、vAB=vB-VAという数式から相対速度が求められます。
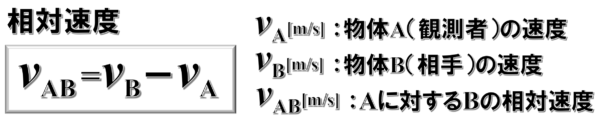
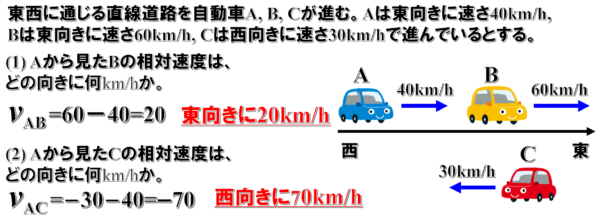
例えば、東西に通じる直線道路を自動車A、B、Cが進んでいて、Aは東向きに40km/h、Bは東向きに60km/h、Cは西向きに30km/hで進んでいるとする時
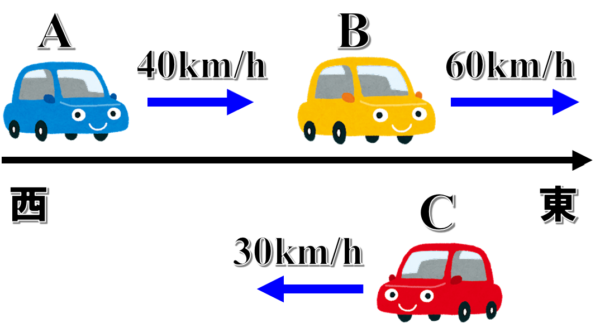
Aから見たBの相対速度vABは、
vAB=60-40=20 したがって、東向きに20km/h
Aから見たCの相対速度vACは、
vAC=-30-40=-70 したがって、西向きに70km/hとなります。

計算する時は、プラスマイナスの符号の取扱いに注意してください。
皆さんは車に乗っている時に、同じ車線を走る車は遅く見えて、反対車線を走る車は早く見えるという経験をしたことがあると思います。このように、相対速度は、移動しながら特定の物体の運動を観測する時に利用する物理量となります。
次の記事
この単元の記事