
はじめに
それでは、前回の問題演習の続きの解説を行っていきます。
今回は、重要問題集47番「鉛直面内の円運動の問題」の(4)からですね。

ここまで来ると、後は容易に問題が解けるようになってきます。
※問題文を掲載すると著作権に抵触するため、重要問題集をお持ちでない方は書店等でお買い求めください。
【後編】鉛直面内の円運動(重要問題集47)

早速いきます。
「レールから離れずに…」というのは、小球がレールに接触しているということですから、接触力が値を持つということですねぇ。つまり、離れないための条件は、垂直抗力が0以上であることです。
そして、もう一つ。

小球が最もレールから離れやすいところはどこですか??
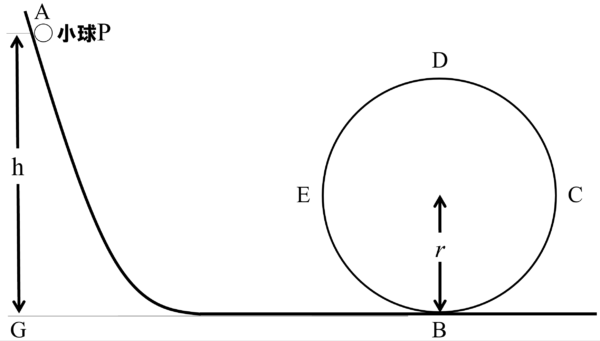
点Dにある小球は、真っ逆さまに落ちていきそうです。したがって、小球が点Dに来た時に離れなければループを1周できます。

つまり、点Dにおける小球Dが受ける垂直抗力が0以上となれば良いわけです。
点Dにおける垂直抗力は(3)で求めました。
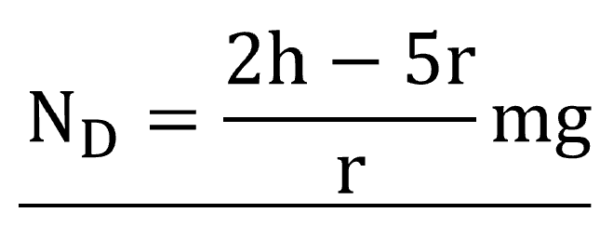
このNDが0以上となるhの最小値が欲しいわけです。よって、hの最小値は次のようになります。


さぁ、ここまで1番、2番、3番、4番と問題を解いてきたわけですが、もしも、この4番が一番最初に来ても、ちゃんと解けますか??

エネルギー保存則と運動方程式を連立すれば良いわけですよね。
「レールから離れずに」とありますから、最も小球が離れそうなのは点Dです。だから、エネルギー保存則から点Dでの速さを求めて、それを運動方程式に代入して垂直抗力求める。

それで良いんです。
ところが、この問題から先に問われると、みんな間違えてしまうんです。

今から小球を点Aから転がすところから始めて解いていくので、どこが間違えているかということを指摘してください。

高さh1で転がした小球Pが点Bで運動エネルギーに置き換わった。それが点Dまで行けばいいと。円の半径がrだから点Bから円の中心までの長さがr。円の中心から点Dまでの長さがr。だから、重力mgに逆らって高さ2rまで行けば良い。それならエネルギー保存則です。だから、次のような式になって…
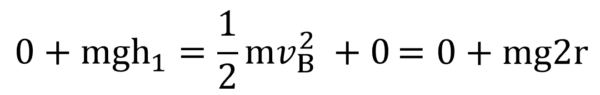
だから結局、この式の一番左の式と右の式からh1を求めるとh1=2r 。

さっきと違ってる…

どこがおかしいのでしょう…??
正しいのは
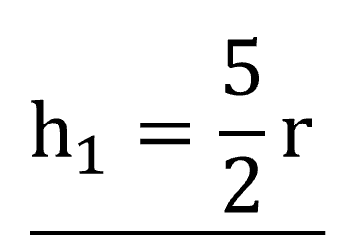
です。

しかし、こういう答えを書く生徒が多いんです。高校3年生になったばかりの時に定期考査や模擬試験を行うと、よくこういうミスをするんです。

こういうことやったことないですか…??
夏の暑い時にバケツに水を入れて、こうグルんって頭の上でバケツを回したりしたことありませんか??

重力に逆らって2r 上まで行けば良いということで先ほど立てた式は、点Dでの運動エネルギーが0でしたから点Dで静止していることになります。

バケツを回転させながら点Dで静止させたら…

これが本物の水だったら、ざばぁ~となって水浸しになってしまいます。バケツを一周させるためには、ある程度勢いをつけないとずぶ濡れになるんです。

ある程度、勢いをつけないと真上を通過できないんです。
だから一見したところ、この解答は合っているように見えますが、そんなことは起きないんです。起きないことに対して、何でこれが間違っているんだといっても仕方ありません。
だから、小球がレールから離れずにループを1周する条件は小球がレールと接触する…

つまり接触力が値を持つための条件。

接触力が値を持つ条件を考えないといけないから、本来は運動方程式から出発しないといけないんです。
そして、点Dを通過する時に最低でもどれくらいの速度を持っていないといけないか??
それなら点Dでは、どれくらいの速度でないといけないのか??
そして、その速度を与えるためにどれくらいの高さから小球を転がさないといけないか??
こういう議論が必要なんです。

もう一度、思い起こしましょう!
円運動。
円運動とは、円の中心方向に落ち込む運動です。

水がざばぁ~っと落ち込んだらいやですよねぇ。
そのために、ある程度の速さを与えないといけないです。
あんまり速さが遅いと本当に落ち込んできますよ!
ってことです。
本当に自分の方に近付いてしまいます。こういう意味ですね。

エネルギーの条件ではないんです。だから、まずは運動方程式で決めてあげなければいけない。この問題では垂直抗力に着目することが大切です。
それでは、残りの問題に移っていきます。
(5)解説
(4)番ではレールから離れずにループを1周するとありましたが、(5)の問題では到達することが条件になっています。(4)の問題では、ぐるっと1周する円運動なので力の条件を考えましたが、ここではその必要はありません。

ですから、点Aより斜面を下ってきて点Cに辿り着いた後に、ヒュ~んと下に落ちてしまったも良いわけです。

重力mgに逆らって半径 r だけ高い点Cに上がる。その時に速度が0。
従って、ここでは力学的エネルギー保存則を考えれば良いわけですが、この問題の場合、

点Cにぎりぎり到達してから逆走した小球は、どこまで戻りますか??

もとの場所です。

rだけ高い位置から下って再びrだけ高い位置に戻ってくる。そして、再び下ったら、また点Cまで来るでしょうねぇ…

もうわかってもらえましたね。
求める高さh2はrになります。

数式を立てるまでもなかったですね。
(6)解説
それでは、(6)に行きます。
レールから離れる点Fにおける小球Pの速さvFを求めよ。
レールから離れるということは、点Fまでは円運動していたわけですよね。だから、点Fまで小球Pは円の中心方向に落ち込んでいたわけです。

そして、点Fに到達した瞬間にレールから離れるわけですから、接触力、つまり垂直抗力が0になります。
したがって、ここでは力の条件を考えることになります。

エネルギー保存則ではないですよ。
離れるということは、これ以降は円運動はしなくなりますが速度が0になるわけではありませんからね。

さぁ、それでは、それらを踏まえて点Fでの運動方程式を考えましょう。
運動方程式を立てるためには、全ての力を書き出さないといけません。
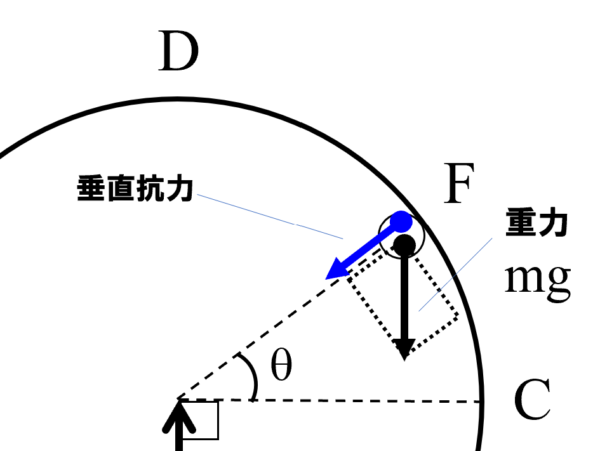
点Fにおいて小球Pにはたらく力は、地球からの重力mgとレールからの垂直抗力です。
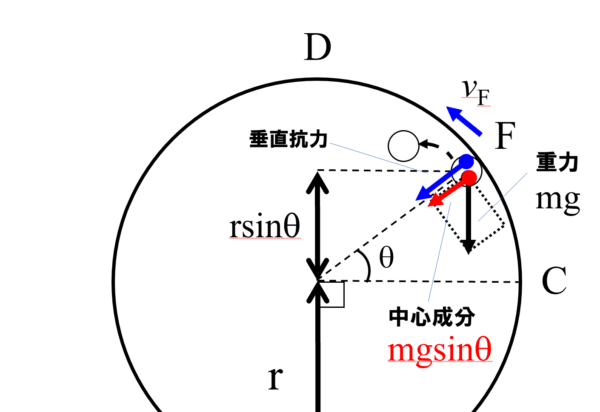
この時、垂直抗力が0になるということが条件でしたから、点Fにおいて小球Pを円の中心方向に落ち込ませる力は、重力mgの半径方向の成分であるmgsinθのみとなります。

θが90度の時、小球Pは真っ逆さまに落ちるはずですからsinθであってますねぇ。
cosθではないので注意してください。
それでは行きます。
![]()
そして、円運動ですから、加速度aは
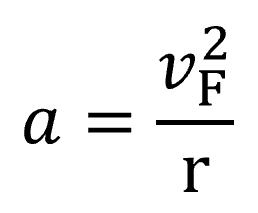
と書けます。
これよりvF は、
![]()
となります。
(7)解説
では、(7)番に行きます。
小球Pは点Fの高さまで上昇して、vFという速さを持つ。そうなるためには点Aの高さhFがどうなっていなければならないか?
と、問うているわけです。
点Bを基準とした点Fの高さを求めておくと、点Fは、半径rの高さから、さらにrsinθ 上にあるわけですから、r (1+sinθ)です。
点Aから重力mgという下向きの力を距離 hFの間に受けたために、点Bを通過した物体は重力mgに逆らって点Fの高さまでやってきた。

したがって、ここで考えるべきは力の距離的効果、力学的エネルギー保存則です。
水平面GBを高さの基準にすると、点Aと点Fにおける力学的エネルギーの関係は次のように書けます。
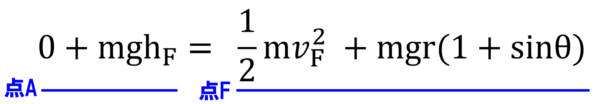
点Fにおいては、高さr(1+sinθ)に相当する位置エネルギーと速さvFに相当する運動エネルギーがあるわけですね。この式より、hFを求めると、こうなります。
![]()

これで、全ての問題が解けました。
(1)~(7)、全ての問題において、エネルギー保存則もしくは運動方程式によって解けたわけですが、そのどちらが解法として適切なのかを見極めることが大切です。
回転する条件、つまり円運動する物体の力の条件について考えるのであれば、運動方程式。
円運動については加速度が特別な表記を持ちますから、力を求める必要があれば、エネルギー保存則から速さを求めて運動方程式に持ち込む。
そういったところに注意して、鉛直面内の円運動の問題の解法を、しっかりと理解してください。


















