はじめに

円運動の内容について、問題解法にまつわる知識から実際の問題の確認までを行っていきます。

ここでは、問題解法に必要な円運動の基本法則について解説します。

この項目では、大学入試問題を解く上での前提となる知識の確認を行っていきます。

要点資料は、以下より閲覧およびダウンロードできます。

主題１．円運動について

今回は円運動に関する基礎知識について解説していきます。

 

円運動では、使うべき式がはっきりとしているので、それほど難しさというものは感じないと思うのですが、しかし…

 

その概念をしっかり理解していかないと、

円運動の後に出てくるテーマである単振動が非常に分かり難くなってしまいます。

 

これは、よく受験生から聞くことなんですが、

っていう声をよく聞きます。

 

その時に、ばねが含まれている問題が苦手だから、

という方法をとっている人が多いんです。

 

 

ばねが苦手な人は「円運動」に戻ることが大事です。

ですから、今回やる円運動ですが、これは、ばねにも大きな影響を与える部分です。

だから、力学の全範囲の勉強はいったん終わったけど、どうしてもばねが苦手だという人は、この時間は、かなり集中して学習してください。

そして、次の回、次の回と進むにつれて、やがてばねの話が出てきますので、

その時に、

 

っていう所を確認すると、ばぁ～っと開けてきます。

したがって、ばねが苦手だから、ばねばかりやるのではなくて、ばねの基礎になっているのは実は円運動ですから、

 

という流れになっていますので、しっかりと円運動は理解してください。

円運動（①速さと加速度）

さぁ、それでは早速、内容に入っていきたいところなんですけれど、

ニュートンが抱いた疑問

その前に、とても有名な逸話として、ニュートンは、りんごが落ちるのを見て、万有引力を発見したという話があります。

ただ、これはどうも、弟子たちがニュートンの功績をたたえるために、逸話としてそのように言ったという風にいわれています。なぜこんな話をしているのかというと、

 

仮にですが、

ニュートンが、リンゴが落ちるのを見て万有引力を発見した。

 

というのが真実であるとするならば、ニュートンはよほど暇だったという事ですね。

確かにニュートンが生まれ育ったウールソープの町は、りんごの木がたくさんあるところらしいです。

しかし、りんごが落ちる瞬間をみるということは、まずありえない。

余程、長時間、リンゴ園に椅子でも持って行って、りんごをじ～っと見ていないと、そういうことは起きません。

このたとえ話のように、ただ単に万有引力を発見したということではないんです。

 

ですから、厳密に言いうと、こういう事なんです。

 

ここなんですね、実は。

確かに、ここにりんごがあったとします。

頭の中で想像してください、手を離します。りんごが下へ落ちていきます。

しかし、月は落ちてこないですね。

 

 

これを考えたんですね。いったいどこに境目があるんだと。

ニュートンも容易に想像したことと思いますが、ものすごい高い山に登って、リンゴをもって、そこで手を離す。

やっぱり落ちますね。

しかし、月は落ちてこない訳ですから。

 

という風に考えたわけですね。実は…。

これは、古代ギリシャ時代、アリストテレスという人が、

というような言い方をした。

要は、

 

 

そういう区別をした。

 

当時は、そのような教科書がまかり通っていた訳です。

 

それを学んだニュートンも、もちろんそういう風に考えていただけれども、

なんていうことを考えついたんです。

 

まずは、結論から申し上げますと、

 

 

 

これが結論なんです。

 

私も授業の中でこういう表現を使うんですが、そうすると生徒たちがポカンとするんです。

 

と。

 

 

地球に向かって落ち続けているんですね。これが月の運動なんです。

ですから、月は何のエネルギーを使うこともなく、地球の周りをぐるぐると回ることができる。

 

人工衛星が永遠と地球の周りをまわっているのはそのためですね。

 

さぁ、だんだんと話が見えてきました。

円運動のお話ですから、今私がたとえ話として、月の話とか、人工衛星の話をしました。

 

円運動と角速度

それでは、早速入っていきましょう。

ニュートンは、等加速度運動という地上界の直線運動について、式を作り上げることに成功しました。

「力」の方から、「加速度」というものを考え、さらに加速度というのは、「単位時間当たりの速度変化量である。」ということから、時間と共に、「速度」や「変位」がどうなるかという式を作り上げました。

そこで彼は、天上界に目を向けたわけですね。

そして、

 

ということになります。

 

それについて、

 

こういう風に考えたわけですね。

そこでまずは、速さについて考えました。

 

速さ…、速度ではないので注意してください。

 

グルグルグルグル、一定の速さで回っているもの、

 

こういう風に考えました。

 

その時に、円運動の大きな特徴は何かって言うと、

 

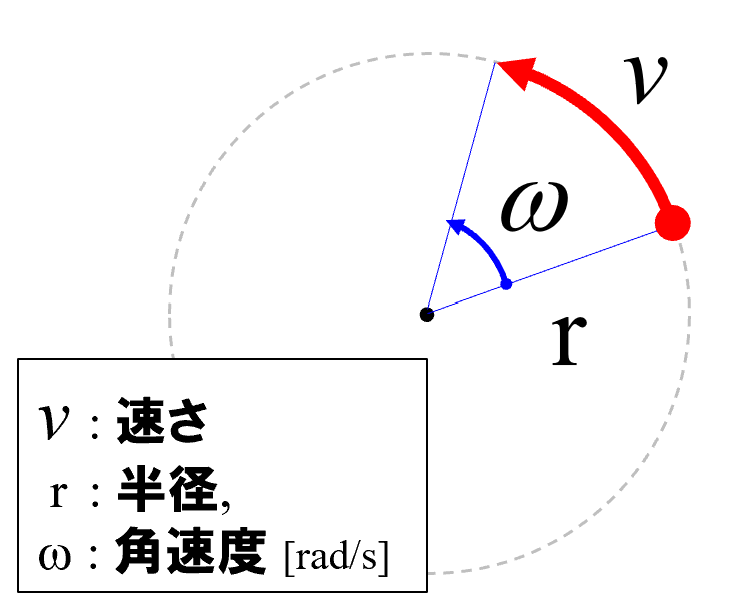
ですから、グルっと回るという式を立ててみたんです。

やってみましょう。

 

 

こうやって書くと、それぞれの文字が何を表しているか、よくわかると思います。
ｖは円運動の速さです。Tは１周回るのに必要な時間です。簡単な言葉で言えば周期。

ですから、

 

 

だから、グルっと１周まわったという式なんです。

 

しかし、もう一つあるんです。それが、これです。

Tっていうのは、先ほどと同じです。w、これは角速度と呼ばれている量です。角速度。

 

角速度というのは、

 

という量です。

 

 

大丈夫ですよね。

 

 

いずれも、グルっと１周まわる式です。

 

この式を連立させたらいいわけですが、ちょっとその前に、このwという量について補足します。

 

角速度。小学校の時くらいに、

 

って観察した時のものです。それが角速度です。

 

これはニュートンが考え出した物理量なんですが、ニュートンは月の運動を見ていた訳です。

 

ところが夜空を見上げて、じっと見てても

 

 

そうやって、w、角速度という物理量をニュートンは導入してきた訳です。

円運動の速さ

さぁ、それでは話を進めて行きましょう。

 

実は、この式を連立するために、割り算をしたんです。

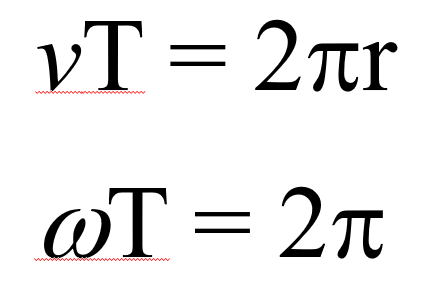
やってみましょう。ここ割り算ですよ。

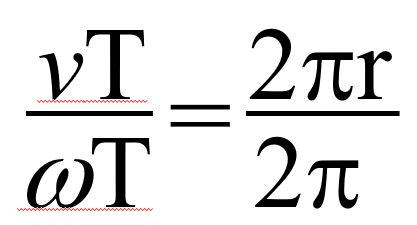
するとTが消えます。よって左辺は、w/v 。

右辺を割り算すると。2pが消えます。

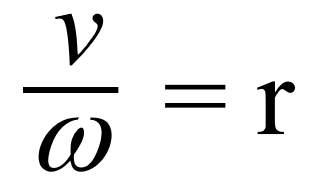
分数の形はわかりにくいので整理すると

出てきました。

もう勉強をし終わっている人は、この式はご存知だと思います。

 

 

v=rwってのを証明することは、そんなに難しいことではないんです。

円があります。１秒間にv[m]進みます。その時に１秒間にwという角度進むわけです。その時、半径はｒです。

そうすると、円弧の長さというのは、長さr×ラジアン単位の角度w だから、v=rwになるんです。

 

これで出来ます。

 

それは、なぜなのかと言うと、

って聞くんですよ。

 

その時に、

 

って、なかなか言ってくれないんです。

 

 

それでおしまいです。

 

 

ですから、これは、

「回るという意味を持つんだよ」

 

っていうことがわかんないといけません。

 

グルっと回るという式（vT=2pr）、グルっと回るという式(wT=2p)。連立をしました。

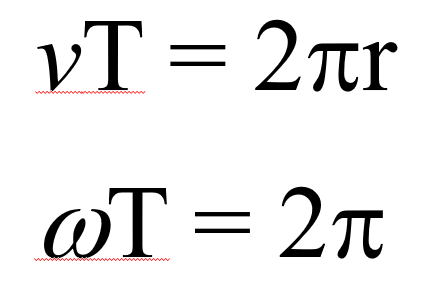
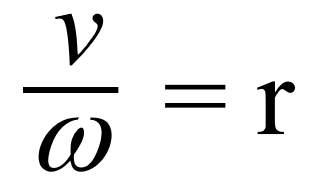
その時に、Tが消え、2pが消えた。

 

すなわち、１周まわる時間が消え、１周の角度が消えました。

 

ということは、「グルっと１周」って言うのはなくていいということです。

 

 

グルっと１周まわるという式を連立して、グルっと１周がなくなったんです。

消えていったんです。

 

 

したがって、

という事です。

 

 

こうやって、意味をちゃんと考えていかないといけません。

 

ですから、

　と、それから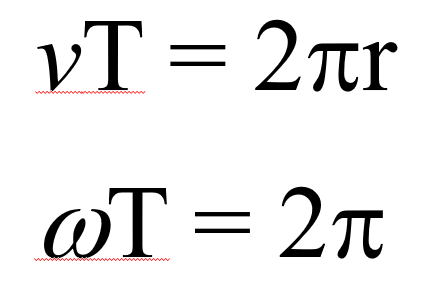

この式を頭の中で分離させてないで下さい。

 

それぞれ１つの意味を持った式です。

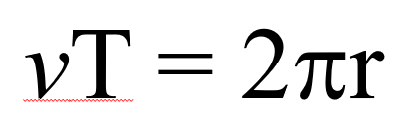
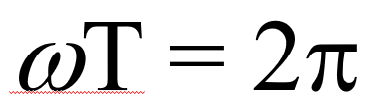
だから、回るという現象に対しては、v=rw は、いつ使っても構いません。

ぐるっと回るについては、

も

も使えます。もちろん、

これも使えます。

そうやって、ちゃんと一つ一つの式に対して意味を理解していくことが大事です。

こうやって、

そこからスタートすることによって、まずは、v = rw という非常に重要な式を導くことに成功しました。