はじめに

それでは今回は、大学入試問題の中で慣性力が活用できる場面について、具体的に学習していきます。慣性力の詳しい説明は、前回の記事を参考にしてください。

 

ということでした。

 

物体を眺める観測者が加速している場合、そのままの状態では、運動の法則ma=Fの関係や作用・反作用の法則が成立しません。しかし、そこに慣性力を仮定してやると、運動の法則や作用・反作用の法則が利用できるというわけですねぇ。

 

 

日常生活において加速した状態で物体を観察するという状況はほとんどないので、慣性力という概念は非常に難しく感じてしまうところですが、その分、大学入試問題においては受験生との間で差が明確に現れやすいところであります。

 大学入試物理 慣性力を用いた解法

今回は、以前に解説した衝突後動く台に乗る物体の（２）番において、慣性力を使った解法を見ていきますが、この前の問題解説の講義ではこんなことを学習しました。

 

そして、時間にｔを直接求める場合は運動量と力積の関係、つまり力の時間的効果が利用できることについて解説しました。

 

 

ということについて、話を進めていきます。

 

 

そのような時には、この問題のように加速度を聞いてみたり時間を聞いてみたりと、小刻みに設問を設けたりするわけですが、これとは異なるパターンとして（２）で距離を求めさせてから、その後に、水平面FG上を動く台の右側にバネなんかおいたりして、そこで単振動について問うてみるなんてこともあります。

 

そうすると、問題としては後半の単振動に対する比重が大きくなってくることが予想されますが、以前解説した通り距離ｄを求める問題については、計算量が多くなってきますので、ここの問題をいかに簡潔に処理して次の問題に移っていくかが、問題を完答する際のポイントになってきます。

さて、それでは、前置きはこのくらいとしておいて、実際に問題を見ていきましょう。

 運動方程式を介さずに距離を求める

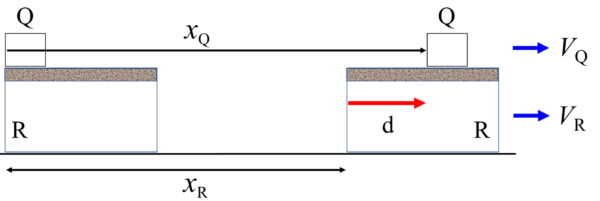
この図にある距離ｄを求めるということについては、以前もお伝えしました。小物体Qと台Rの速度が等しくなる関係を利用して時間ｔを求めてからx_Qとx_Rを求める。そして、その差をとれば良いわけです。時間ｔについては、運動量と力積の関係や運動量保存側から求めることができて、x_Qとx_Rについては、等加速度運動の式もしくは仕事と運動エネルギーの関係から求まります。

 

以前お伝えした方法だと時間ｔを求めてから、x_Q、x_Rを計算するというように個別に式を立てたため、その都度計算式が必要となり計算量が膨れあがっていった訳ですねぇ。

 

それで、今回は直接距離ｄを求めてみる訳ですが、

パッと見、この台R上から小物体Qを眺めた方が、簡単そうですよね。

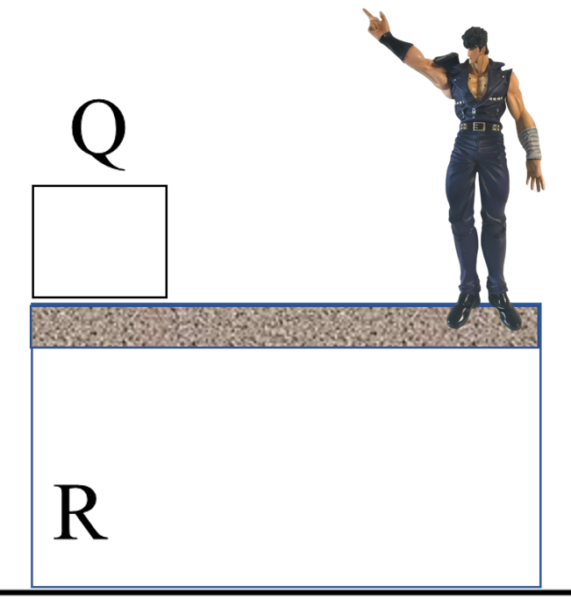
そこで、この小物体Qについて見てみると、

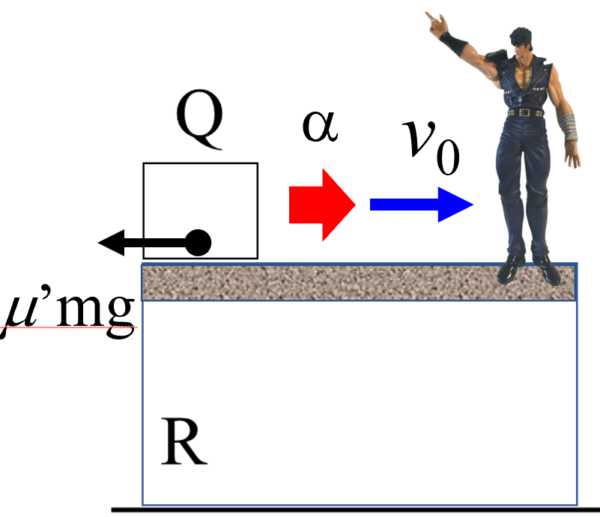
Qには加速度αが生じていて、これは計算すると負になるので減速していることがわかります。その原因となるのが進行方向と逆向きにはたらく動摩擦力 m‘mg です。

このように進めて行くと、やがて解答にたどりつく訳ですが、次のようなミスをする生徒がいます。

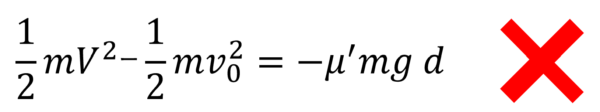
 と立てても、距離ｄは求められません。

 

 

 

 

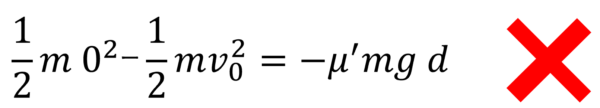
となってしまいそうですが、そのようなことはありません。

 

ですから、運動の法則から導かれた力の距離的効果や力の時間的効果も、当然成立することはありません。

 

 

ニュートンの運動の第２法則である、運動方程式と第３法則の作用・反作用の法則は、無条件に成立するものではありません。そのことをニュートンは理解していたので、その成立条件として運動の第１法則である慣性の法則を唱えたという話を前回しました。

 

 

そこで、今回の観測者に戻りますが、この観測者は加速度bで動く台の上に乗っかっている。したがって、観測者は加速度bで動きながら小物体Qをながめているわけですから、そのままでは運動の法則は使えません。

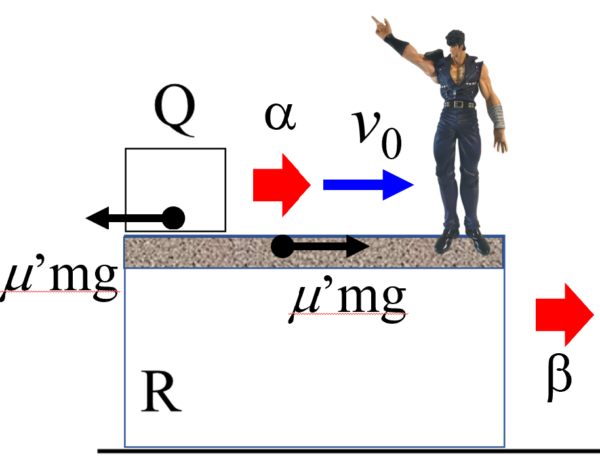
さぁ、そこで登場するのが慣性力です。

というのは、とてももったいないですねぇ。

ですが、慣性力という力を仮定してやると、加速しながら物体を観測していても、運動の法則が成立します。それでは、一度やってみましょう。

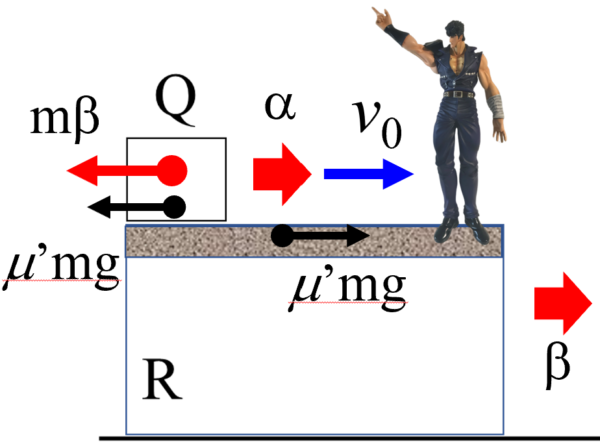
図に示すように、加速度bで動く台Rに乗っかっている観測者から見た小物体Qにはたらく力は、進行方向と逆向きにはたらく動摩擦力の他に加速する台とは逆向きに慣性力mb がはたらくと仮定します。

 

小物体Qの速度については、最初は静止している台の上から見ていたわけですから、v₀です。最終的に台R上で静止した訳ですから、台Rの上からはQは止まって見えますよね。したがって、速度は０となります。これは台Rから見た小物体Qの相対速度に相当します。

 

この間、物体Qが台R上を移動した距離はｄですから、

 

とすれば良いわけですね。

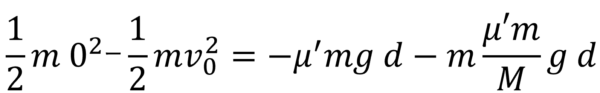
ここには、（２）(a)で求めたβの値を代入しています。

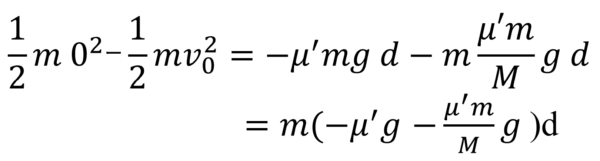
この式から、ｄを求めると･･･

 

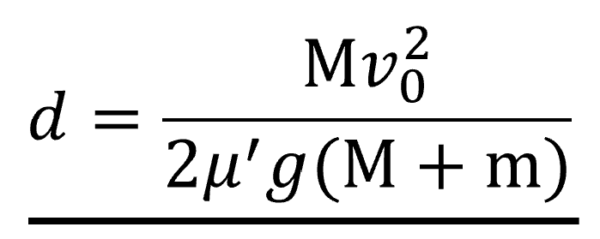
時間ｔやx_Qやx_Rを求めなくても、距離が求められました。

これが、慣性力を使った解法になります。

 

ニュートンの運動の法則が無条件に使えないというのは、我々受験生にとっては、非常に厳しいわけですが、しかし、成立条件をしっかりと理解して観測する立場を明確にしてやれば、あっさりと求められてしまいます。

 

 

ここの部分です（青い部分）。

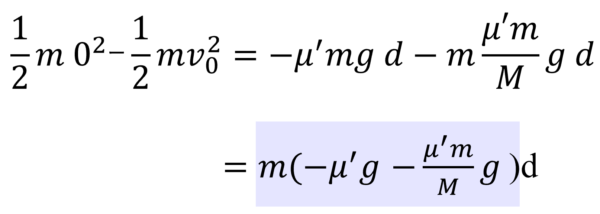
ここは仕事の定義の力かける距離に相当する部分で、まずｄは距離に相当することはわかりますよね。次に力の部分ですが、力は質量かける加速度ですから、この時の質量はｍ。そして、カッコ内は加速度に相当する部分ですが、ここを和訳してみると、α-β、つまり台Rから見た小物体Qの加速度となっています。

 

皆さんは、速度Vｂで動く物体から見た、速度Vaで動く物体の相対速度はいくらかと聞かれたら、Va-Vbとやりますよね。

 

今回の問題では、加速度bで動く台Rから見た、加速度aで動く小物体Qの相対加速度を考えていたわけなんです。

 

加速しながら物体を観測する場合、これを非慣性系と言いましたね。

この非慣性系においては、物体にはたらく力には慣性力を考えようという話でしたが、加速度に着目して考えるのであれば相対加速度を考えなければならないということです。

 

したがって、

 

ということです。

 

はい。これで、慣性力を利用した解法についての説明は以上となりますが、計算量に大きな違いがあることをわかっていただけたと思います。

ｖ－ｔグラフを用いた解法

今回解説した問題については、さらに別解としてｖ－ｔグラフの面積から求めるという解法があります。これについても少しだけ触れておきます。

 解法そのものは一度説明を聞けば

 

と、確かに理解はできると思います。

しかし、ここで問題なのは

 

という疑問が浮かんできます。

 

それについて高校の教科書の範囲内で説明をするのであれば…

 

ということです。

ｖ－ｔグラフに、v ＝v₀+at という一次関数を書き込んで、初速度v₀、一定の加速度aでt秒間進んだときの距離を、v₀t という四角形の面積と1/2at²という三角形の面積を足し合わせることで、x = v₀t+1/2at²という式を導きましたねぇ。

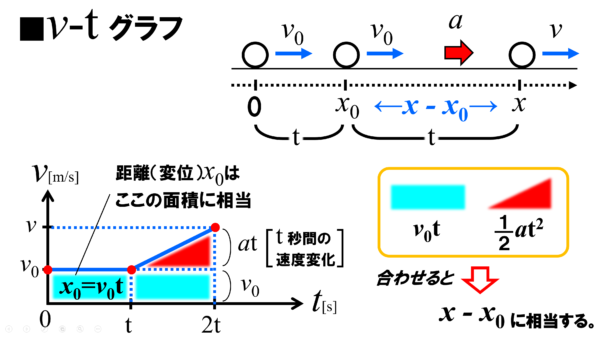
あれを、この問題でも使ったんです。

 

したがって、等加速度運動の問題の解法として、ｖ－ｔグラフの面積を求めるのは、とても有効な手段として機能するわけです。皆さんは、高校の数学で関数のグラフから面積を求める時に積分するということを学習したと思います。

 

大学に入ると物理学については、より数学的な議論が必要になってきますので、今回のような問題でしたら、加速度α、βをそれぞれ積分して、小物体Qと台Rの初速度は、それぞれv_o, 0であることを初期条件として、ｔ秒後の速度が等しいという条件から速度と時間を求めます。

そして、その速度をｔ秒間という区間において積分してやれば、距離が求まります。大学課程においては、数式を用いた考え方の方が主流になってきます。

しかし、高等学校の物理については、微積を用いた解法を求められておりません。それに加えて、物理学が好きでとことん学びたいという人であれば話は別ですが、

大学受験を控えている皆さんは、物理だけを勉強していれば良いわけではありません。したがって、大学に入ってから学ぶ教養については、今は立ち入らない方がいいでしょう。受験本番までに残された時間を、各受験教科にバランス良く配分していってください。

 

さて、これで今回の講義は終了となりますが･、大学の立場からすると、できるだけ優秀な学生に入学して欲しいという想いがあります。そのような想いを込めて大学入試問題を作成するわけですが、

 

それだけでなく大学によっては、

 

より本質に迫ったスマートな解決策を選べる受験生

 

という風に、求める人材のハードルを上げてくることがあります。

 

 

大学入試問題とはいっても、高校の範囲から逸脱した問題はありません。だから、じっくり時間をかけることさえできれば、何とか解ける問題が大半ですが、そこに時間的な制限が掛ってくると一転して厳しい状況に追い込まれてしまいます。

 

そのような場面にあっても、より本質的なところにアプローチして速やかに問題を解決する力。今回の慣性力を用いた解法は高校物理の中では高度な内容になってきますが、頑張って学習して是非自分のものにしてください。