危険物資格取得のための高校化学No.18 原子の相対質量

この先、化学物質の数量的な関係を吟味していくときに、このような数字ばかりだと、とても扱いにくい。そこで登場するのが、今から紹介する「相対質量」という訳だ。

それでは、
今回のポイントを確認しよう。

以上の３つだ。

■ポイント１．原子１個の（絶対）質量は、とても小さく扱いにくい。

まず、1つ目のポイントについてだが、実際に測定した原子の質量のことを、「絶対質量」という。
原子１個の質量は、とても小さく扱いにくいことは、冒頭で説明した通りだ。
そこで、計算を簡単にするために、原子の質量を我々にとって扱いやすい数字に置き換えることを考えてみる。

■ポイント２：炭素原子の（相対）質量を１２と定め、これを基準とする。

それが、ポイントの2つ目の炭素原子の（相対）質量を１２と定め、これを基準とするということだ。今から、これについて説明しよう。

原子の質量を扱うときに、我々が扱いにくいと感じるものは、この少数を含む数値と指数だ。

だから、生命にとって欠かせない物質の１つである炭素原子の質量を１２と定めた。そして、他の原子については、炭素原子を基準にしたときの割合を考えることにした。

この

という。

ちなみに、当初は生命にとって欠かせない物質である酸素を基準としていたが、科学者たちの事情によって炭素に切り替えられることになった。

さて、今、炭素原子を基準に定めたから、この基準を参考にして他の原子の相対質量を計算によって求めていきたい。

だが、その前に思い出してほしいことがある。炭素原子の１２という数字から、何か連想できるものはないかね？

そう質量数だ。質量数は陽子と中性子の個数を数えたものだったな。

全ての原子は、陽子と中性子と電子で出来ており、電子の質量は無視できるほど軽いという話をしたことを思い出してほしい。ということは、他の原子の相対質量も、質量数に近い値になることが予想できるな。

例えば、酸素原子の相対質量は、質量数に着目すれば、だいたい１６くらいと考えられる。

これから酸素原子の相対質量を計算によって求めていくが、予め答えになりそうな値を予測しておくと、計算ミスを防ぐことが出来る。

現実の炭素原子の質量はとても小さく、数字で表現しても扱いにくい。そこで、質量数に着目して相対質量を１２と定めこれを基準とした。こうしておくと、我々にとって常識的な数字で、物質の大小関係を比較できるから便利なのだ。

二酸化炭素が生成する化学反応式であれば、炭素原子の相対質量は１２で酸素分子は酸素原子が大体１６くらいだから、１２プラス１６×２で４４となる。

とまぁ、こんな感じで最初の計算に比べて、数字の大小関係とか分かり易くなっているだろう。

実際の質量を知りたいときは、炭素原子を基準にして、相対質量の値から、全ての物質の質量を実際の値に変換することが出来る。

■ポイント３．他の原子の相対質量を求めてみる。

今から実際に、酸素原子の相対質量を求めてみよう。

まずは、酸素原子の相対質量をxとしておこう。
酸素原子の相対質量を求めるというのは、炭素原子の相対質量を基準の１２と定めた時に、酸素原子はいくつになるかを求めることだ。

これについては、炭素原子を基準とした酸素原子の割合を元に考えていく。割合とは、基準となるものに対して、着目する量は何倍なるかということだ。

例えば、６００ｇのりんごの質量は２００ｇのみかんの何倍かという問いであれば、
着目する量はりんご６００ｇ、基準の量はみかん２００ｇだ。

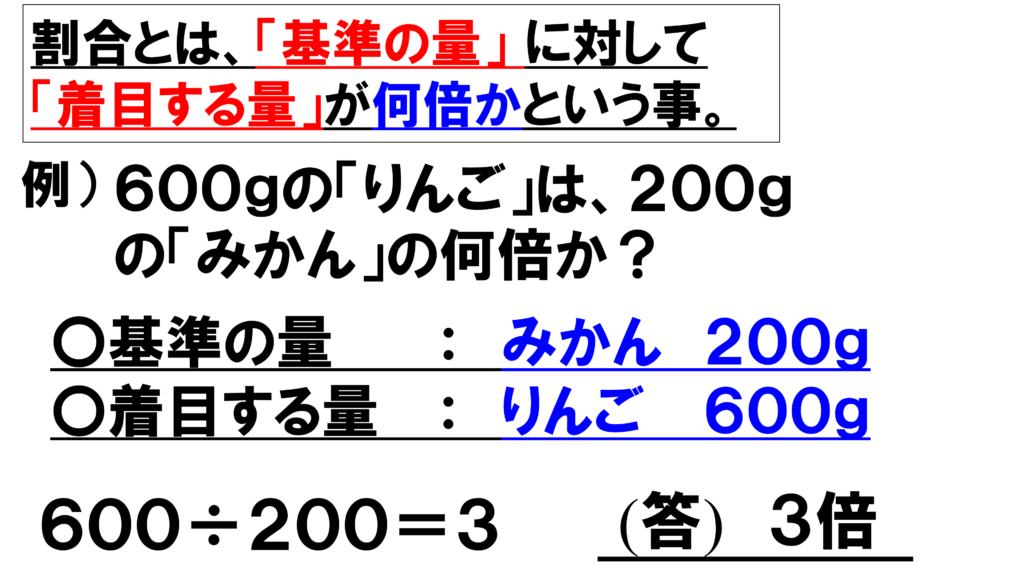
この場合だと、６００ｇのりんごの質量を２００ｇのみかんの質量で割って3倍と答えるだろう。

この計算を例にして酸素原子の質量が、炭素原子の何倍かを考えてみる。
まず絶対質量を使って計算式を立てると、2.656 × 10^－23　÷　1.993 × 10^－23と書ける。
そして相対質量で表現すると、ｘ÷１２となる。

この２つの式は、それぞれ絶対質量と相対質量を元にして立てた式だが、酸素原子と炭素原子の質量の割合に関する式だから、二つの式の計算結果が等しくなければならない。

ということで、２つの式の計算結果が等しくなるという計算式を立てて　ｘを求めると、最終的にｘは、小数点第4位で四捨五入すると15.995となる。

どうだい、１６に近い数字になっただろ。最後の５を四捨五入すれば、確かに１６になる。

今日の講義は、ここまでとしておこう。それでは次回の授業でまた会おう。

◎異なる単元の学習は、こちらのガイドを活用ください。