はじめに
それでは、波の例題の解説を行います。
□基本事項の確認はこちら
①波の表し方(y-x図、y-t図)
②波動に関する量(講義編:前編)
③波動に関する量(講義編:後編)
□動画による解説はこちら↓↓↓
波の例題解説
図はx軸正の方向に進む波の時刻t=0における波形のグラフであるとあります。
物理の問題としては、こういう風な形で出てきます。

この図を見たときに、皆さんはすぐに頭の中で、「おっ、写真だな!」っと、前回の授業の内容を思い出してください。
みなさんがたとえば友達の家に遊びに行ったとします。
それで、友達の家に遊びに行って昔の写真を見せてもらったとしましょう。

そうしたら、どんな会話になりますか?

これいつの?

小学校1年の時なんだ。
とかなそんな話になるでしょう。
写真には時間の情報がありません。

だから聞くんですねぇ・・・。
私たちも同じです。

おっ、波形のグラフだ。

いつの?
って、
そうしたら、時刻t=0におけるって書いてあります。
だから、時間の情報をまずはしっかり問題文の中から得るということが大切です。
それでは、問いを見ていきましょう。
(1)媒質の速さが0となる点のx座標を求めなさい。
(2)媒質の速さが、y軸正の方向に最大の点のx座標を求めなさい。
(3)原点の媒質の振動の様子をグラフに示してみなさい。
ただし、波の速さは、2m/sである。
1番が媒質の速さ、そして2番も媒質の速さ・・・。

1番と2番は、同じことを聞いてる訳です。
片方は0の時で、片方は最大の時です。

そして、3番は、原点の媒質の振動の様子はどうなってますか…??

なんだ!
みんな動きじゃないか!?
たった1枚の写真だけ渡しといて、みんな動きを言えって言ってるんです。

それなら、連射しないといけません。
では、やってみましょう。
(1)解説
まずは1番からです。
媒質の速さが0となる点のx座標を求めなさい。
ということは、ロープのどこかに赤い印がしてあるんです。
その赤い印が、速さが0のところにあるんです。

そのx座標は、どこですか?
って言ってるんです。
高等学校で学習する波の波源は、単振動を行っています。
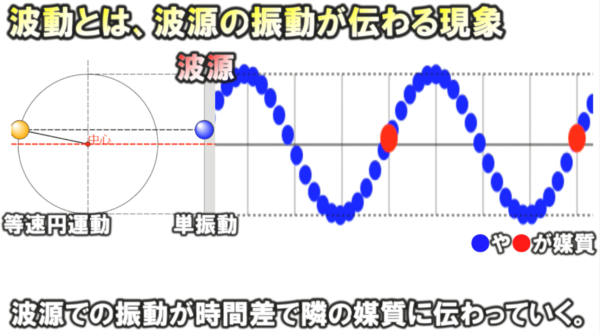
波源での振動が、周囲の媒質に伝わることで、各点での媒質は、時間差で波源と同じ単振動を行います。
この単振動が伝わる様子を眺めていると、あたかも波が右向きに伝わっているように見えて、その波形が伝わる速さのことを波の速さと言いました。

ただ、ここで間違ってはいけないのは…

今回問われているのは、媒質の振動の速さなので、右向きに移動する波形の速さが聞かれているのではなくて、各点で上下に振動している媒質の速さのことです。
その点だけ注意してください。
それで、1番では、媒質の速さが0になる場所が聞かれているわけですが、それがどのような場所かというと、波源の振動をよく見て下さい。
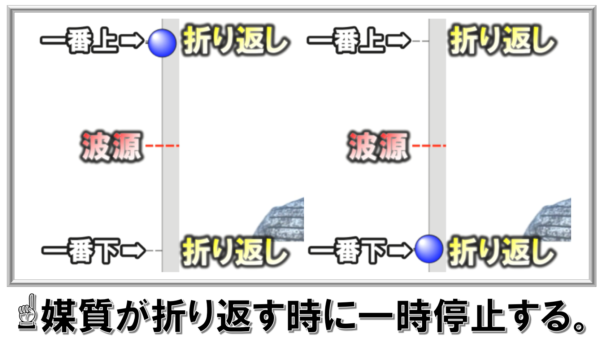
媒質が一番上まで行って折り返す時、それから一番下に行って折り返す時、この時に方向転換するために一端止まっています。

進行方向が逆向きになるということは、一時停止する瞬間があるということです。
だから、速さが0になる点は、一番上か一番したになります。
つまり変位の大きさが最大になるところです。
ということで、1番は媒質の動きを答えないといけないのですが、ここは、波形を動かさなくてもすぐに答えられます。
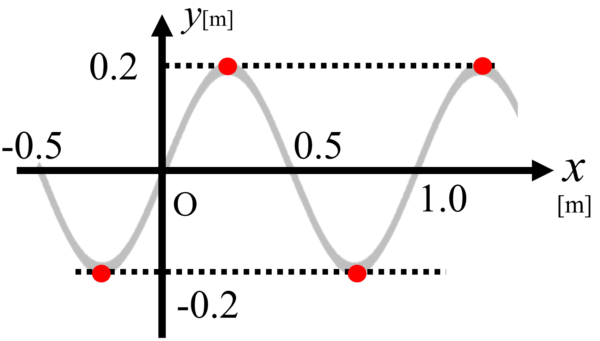
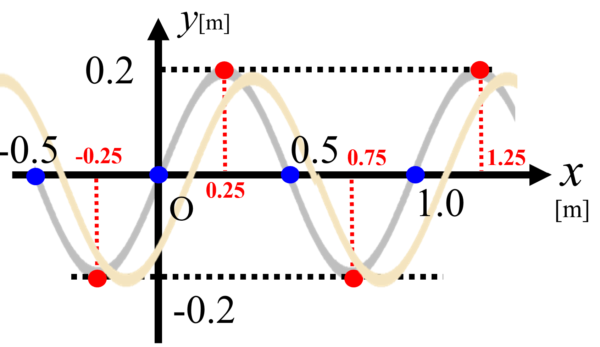
したがって、上の図の赤い印の点が媒質の速さが0になるところです。

ですから、x=マイナス0.25、
それから、0.25、0.75、1.25m。
こういう場所になります。
これが1番の解答です。

(2)解説
それでは、今度は2番です。
媒質の速さがy方向に最大になる点のx座標を求めなさい。

これは、完全に動きが分からないと無理ですねえ…
いったん止まるっていうところではありませんから。

ですから、
連射してあげましょう。
図の写真よりも、少し時間が経った時のグラフを手に入れましょう。


速さが最大になる場所はどこか・・・?
これは力学で単振動を学習していないので、数学的に示すことは今は出来ません。

だから、ここでは単振動の動きを見て、ここが一番速くなっているという風に理解してください。
そうやって、波源の振動を見てみると、

真ん中を通過する時に最大の速さを持っていそうだ…
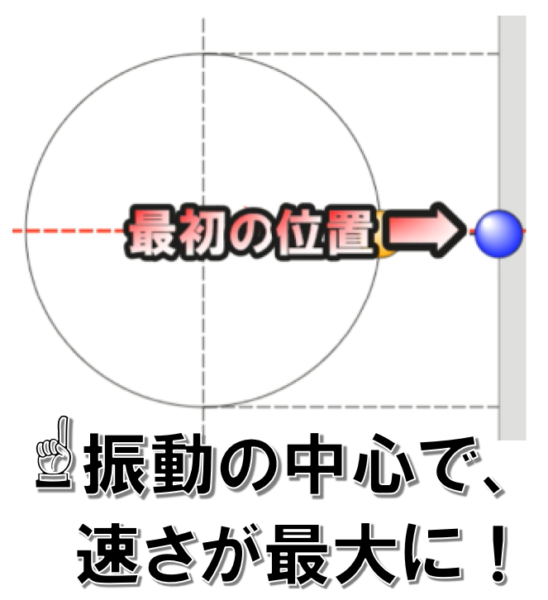
ということが確認できます。
それが、どんなところかを確認してみます。(下図の青い印)
波の写真を連射して並べたおかげで、次の図のように青い印の動きが、どんな動きをしているかということがわかります。
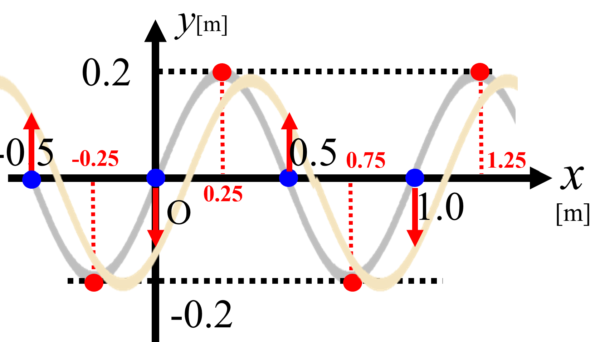
ですから、グラフを波の進行方向に少しずらして媒質の動きを見れば良い。
ここでは、y軸正の方向に動く場所を選ばないといけないので、

y軸正方向に最も大きな速さを持っているのは-0.5の場所と0.5の場所であるとすると・・・
これだけが答えということになります。

ここも大きな速さを持ってるんですが、これはy軸負の方向に進んでいるいうことが分かります。

どうですか?
必ず、波の問題が出た時にはやらないといけないことがあるんです。

それが何かっていうと、写真と、赤い印や青い印の動きという2つの言葉を使って、与えられたグラフや問題文を書き直してみることなんです。
写真とか赤い印の動きっていう風にしておくと、捉えにくい波動であっても、とても簡単に頭の中が整理できるようになります。
だから、そういう風に言葉を書き換えることによって、
グラフに対して何をすれば良いか?
何を読み取れば良いか?
っていうことが、ごく自然に、分かってきます。

「受験のテクニックとして覚えるとか、こう聞かれたらこう解け!」とかではないですよね。

そう解くべきですよね。
どちらかというと・・・。

そういうことを考えることが物理という学問です。
それでは最後の問題です。
(3)解説
これも、よく出る問題で多くの人が間違えるところです。
原点の媒質の振動の様子をグラフに示してみなさい。
ただし、波の速さは、2m/sである。
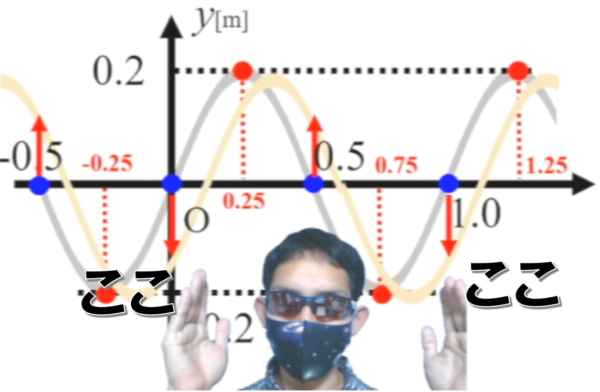
まずは原点の媒質の振動の様子が知りたいということですから、早速、原点に青い印をつけるわけですが、青い印は2番の問題で既につけてあります。

そうすると時刻 t=0では0にあったものが、ちょっと時間が経つと下へ向かっていることが確認できます。

ちょっと時間が経つと、下へ向かう‥‥。

これで準備完了です。
今からグラフの作図に移ります。
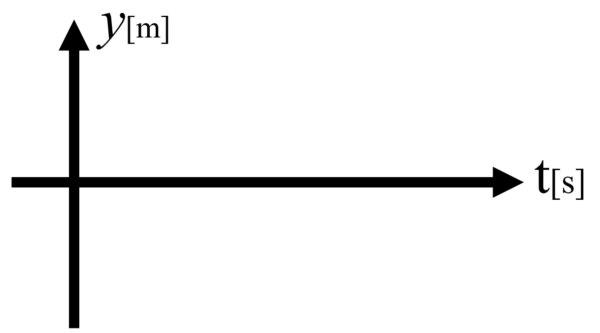
横軸は時間です。縦軸はyのままで。。
まず、t=0では、波源は原点にありました。

しかし、ちょっと時間が経った時に青い印はどこへ行ったかというと…
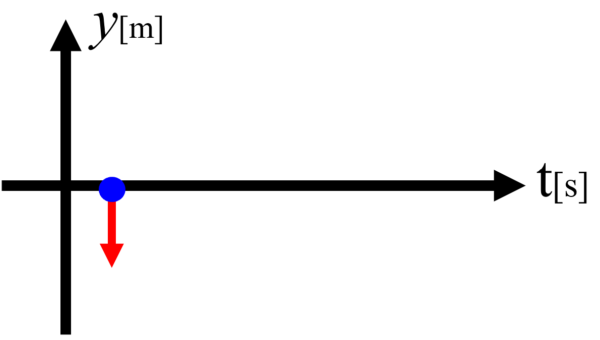

矢印の長さの分だけ、
下へ行きました・・・。

ということは、きっと、こんなグラフになるはずだ!
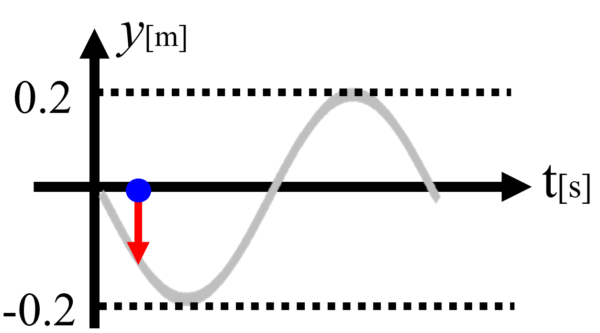
そして、当然振幅は-0.2です。

それじゃあ、後は周期を求めるだけです。
周期Tは、次のようになります。
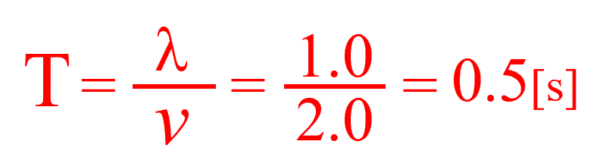
従って、解答は次のようになります。

これは、よく出てくる問題なので注意してください。
注意点とまとめ
それでは、最後の解説に行きます。
実際に、(3)では、こういう風なグラフはかけますが、

問題文に与えられた図がこういう風な正弦波のカーブになってるから、


これだって同じだろう?
ってやってしまう人がいっぱいいるんです。

そんなことしたら絶対にいけません。

じゃあ、どんなことをすればいいの?
最後にまとめましょう。簡単です。

写真と赤い印や青い印に全部置き直そう!
って言ってるんです。

そうすると…
今写真がありますよ。
原点に青い印有りますよ。

青い印どう動いたかグラフで表しなさい!
ってわけです。
そうしたら…

その青い印が最初は原点にあったけど、1回下に下がって、ぐうっと上に上がったんだ。
そうやって考えて行くとグラフが描けます。

波の問題は動きが見えないからなかなか解けない!
と、不平不満を言わずに。見えるように努力する。
そうやっていくと、波の分野っていうのは非常に簡単に解くことができるんです。
ぜひ一度皆さんもやってみてください。

















