はじめに
前回に引き続き、波について講義を進めてきます。
□前回の講義

今回は、前回学習した波を表すための様々な量を利用しながら、「波というものをどのような形で表現していけばよいのか?」
という話をしていきます。
ただ、表現すると言っても言葉が難しい部分があるので、具体的にどういうことをするのかを簡単にお伝えしようと思います。
たとえば、こんな風に考えてみてください。
公園に1本ロープがあります。そして、そこに波を作ります。


それで、公園にいない人にどんな波が出来るかをどうやって説明するのか?
そういう風に考えてみてください。
そんな時に、
どんな方法でそれを伝えることができるのか?
ということを考えていきます。
しかし、これはそれ程簡単なことではないんです。
実は、波というのは、もともとピンと張ってあったロープが、どれくらい変位しているか?

これがわかりさえすれば、波を伝えたことになるんですが、この変位というのは、場所が決まれば決まるかというと、そうではありません。
場所というのは、ロープを持っているところから、例えば5m離れた場所、
という特定の場所。
その場所が決まれば、必ず変位が決まるかというと必ずそうじゃありません。
ロープは時間と共に動いています。
それじゃあ、時間が決まれば、全ての変位が決まるかというとそうでもありません。
場所、時間、それぞれによって変位は異なってくるわけです。
だから、1カ所だけ見てやると、波が伝わるかというとそうではありません。
じゃあ、1つの時間を見てやると良いかというとそうでもありません。

こういった事を、いかに外に伝えるのかって言うのは、非常に難しいことなんです。
これから、その事についてじっくりと考えていきたいと思います。
それで、今回は「波の表し方」ということでやっていきます。
波の表し方

どうやって波を表していけば良いだろうか?
ほとんどの教科書にはこういう題名の項目が必ずあって、波の中では非常に重要な場所になります。

ただ、さっきも言った通り、波というのは例えば、ある瞬間を見れば、こうなんですが…

今見ている波形は、時間の経過とともに、どんどんどんどん流れていくわけです。

そうすると、ある1カ所を見ても、時間が決まらない限り変位というのは決まってこないんです。
例えば場所をxで表すとします。
時間をtで表す時、xもtもそれぞれ変化します。
その変化に対して、変位yというのが決まってきます。

言ってみれば、変位yというのは、xとtによる関数なわけです。

少し、難しい話になってきましたが、敢えてもう少し難しい表現をします。
数学が得意な人は、わかると思います。
xとtが独立に動く、独立変数ですね。その独立する2つの変数によってyが決まってくる。

yは従属変数と言います。
すなわち、3つの変数を扱わなければならなくなってきます。

こんなことを言い始めると、難しく感じると思いますが、何でこんなことを言い始めたのかと言いますと…
もし仮に、これ(変数t)が無かったら、2変数です。

皆さんはすぐにわかります。
例えば、y=x2…と言ったら、
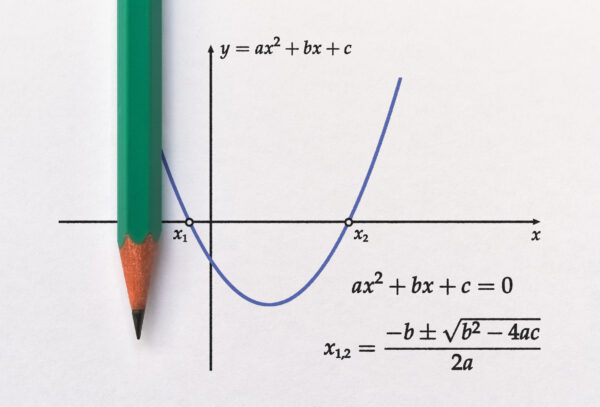

頭の中でスゥ~っと放物線のグラフを描けるんじゃないですか?
ところが、それにもう1個変数があります。

例えば、zっていう変数があると言われただけで、もうどんなグラフを書いていいかわからなくなってしまいますねぇ…
3変数関数っていうのは、非常に扱いづらいものなんです。

そこで何をするのか?
xも動きます、tも動きます。それに伴って、yも動きます。
yも変数です。

これが分かり難い !!
ということは、例えば、

時間よ…止まれ !!
ってやろうってわけなんです。
つまり、固定してやるんです。

これを固定すると、xとyの変数になりますから、簡単に理解することが出来ます。

こういうのを、波のy-xグラフと言います。
という事は、もう一つ見方があります。

今度は、xを固定する見方です。

そうすると、y-tグラフが得られます。
全部が動くと大変なので、何か1つを固定して考える。
こういう考え方をするわけです。
y-xグラフ(y-x図)
そこで、まず最初にY-Xグラフというものを扱ってみたいと思います。
y-xグラフというけれども、それは tを固定したんです。

皆さんが持っている教科書や参考書にはy-xグラフと書いてあると思いますが、y-xグラフという題名が大切なのではありません。
本当はyというのは、xとtで決まるのに、わざわざy-xにしたという事は、
tが固定されている。
っていう意味です。

縦軸に変位yをとり、横軸xをとって、適当に波を書いてみます。
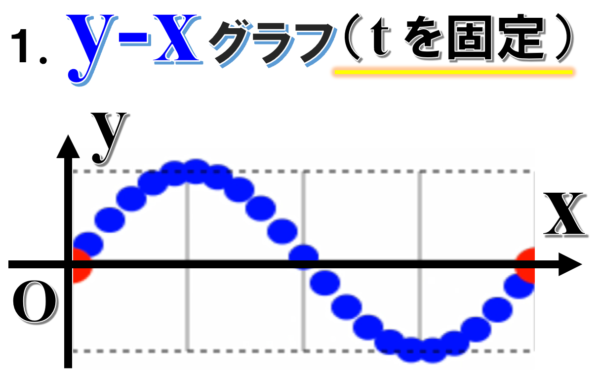

このグラフは、なんですか?
って聞くと、

えっ!?
ってなるかもしれません。

何ですかって先生が書いたんじゃないですか?
って…。

しかし、「これが一体何を表すものなのか?」ということがわからないといけません。
ところが、

何を表すんですか?
って聞くと、

それは、y-xグラフよ。tを固定してあるんですよ。
それだけで、話が終わってしまう人がいるんです。

皆さんについては、中学生にわかるように説明できるようになってください。

どうすればいいか?

それは…、ここ(tを固定)なんです。
tを固定です。ここは非常に大切なところです。

ゆっくり進めて行きます。
tが固定できるものを、皆さんも持っていると思います。

さぁ、それは何でしょう?
カメラです。

ビデオカメラじゃないですよ。

写真のほうです。

皆さんは、自分が赤ちゃんの時の顔を見ることが出来ますよね。


お父さんやお母さんが、「まぁ可愛い子だねぇ…」って、パシャって撮ったんです。
その時点で、時間が止まったんです。

ですから、これは、波の写真なんです。
とても大切な概念です。
まずは自分の部屋に出来ている波を、外部の人に伝えたい。
その一つの方法として、今出来上がっている波を、写真で撮る。
そしたら、こんな写真が出来上がった。

ここの部屋に出来上がっている波っていうのは、こんな波です。
って、
写真を見せてあげるんです。
まず部屋の外にいる人に対して、波を伝えるという意味では、そういう使い方があるということです。

ですから、波の写真っていうことは、これは、少しカッコつけた言葉で波形のグラフという考え方になることは分かってもらえると思います。
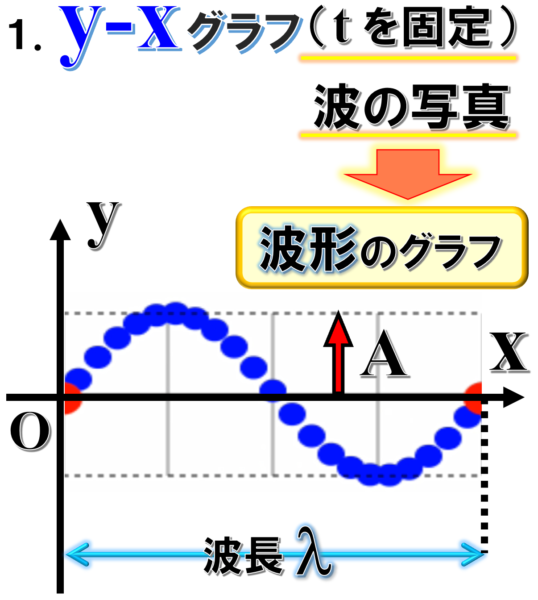

見たまんまのロープが、どうなっているか?
その波の形を表しているんです。
だから、写真の縮図や縮尺さえ分かれば、前回勉強した波長や振幅はすぐに分かるということになります。
波の写真っていう考え方をしっかりともっておいてください。
ここで、もう少し話を深めていかなければいけないんですが、ひと先ずこのままで置いといて、次の話に移ります。
y-tグラフ(y-t図)
それでは今度は、もう一つやらなければいけないことがあります。

それが2番目として、y-tグラフです。
xを固定です。

これは何て言ったら良いのでしょうか?

xを固定するってどういうことでしょうか?

難しいですねぇ。
具体的に考えて行きましょう。
公園の柱にロープが結んであります。

そして、反対側のロープを持ちます。そして、波を起こします。
すると波が伝わっていきます。

それで、こちら側から、パシャっと写真を1枚撮りましたよ!

っていうのが、さっきやったy-xグラフです。

今回の、xを固定するってどういうことですか?
たとえば、私が手で持っている場所。これを波源としましょう。
そして波源から5m離れた場所を固定しましょう。


5m離れたところをぎゅっと固定するという意味ではありません。
場所を確定してしまおうということです。

y-tグラフですから、横軸はtです。
時間と共にどう動くか?
っていう量です。

ということは、例えば、「私の手から5m離れたところのロープっていうのは、どう動いていくか??」っていうのを y-tグラフは表しているんです。
それをここに書くと大変なんで、アニメーションに切り替えて考えていきます。
原点の位置が、ロープを手で持つところで、5m離れたところがここです。

ここに赤いマジックで、赤い印をつけたとします。

それからロープを振動させてみるんです。
そうすると、5m離れたところで赤い印は、上下に動いています。



マジックで赤くぬったところが、すぅ~っと右向きにはいかないですよね。

上下に動いてるんですね。
ですから、ここ(tを固定の下)に入る言葉を入れるとするならば、難しいかもしれませんが、

ロープにつけた赤い印の動きなんです。

分かり難いっている人がいるかもしれません。
確かに、分かり難いと思いますから、なんか例を挙げてみましょう。

何にしましょうか…。

水面に浮かんでいる葉っぱにしましょう?
今、風のない非常に穏やかな湖があって、そこに1枚の葉っぱが浮いてます。

そして、ぽちょんと石を投げます。

そうすると同心円状の波が「わぁ~っ」と広がっていきます。


そのときに、葉っぱはどんな動きをしますか?

葉っぱは時間と共に、その場で上下に動いています。

波乗りみたいにスゥ~とは動いてないですよね。
だから、ここは水面波で言うならば、y-tグラフは「水面に浮かべた葉っぱの動き」と言ってもいいかもしれません。
そうやって、
場所を固定するというものをどうとらえるか?

時間を固定する方が写真で簡単だと思いますが…。
y-tグラフを
「ロープにつけた赤い印の動き!」
とかって言っているけども…

これをもうちょっと理科的な用語を使って表すと、媒質の振動のグラフということになります。
媒質がどんな振動をしているか?
ということです。
だからy-tグラフは、こんなグラフになります。
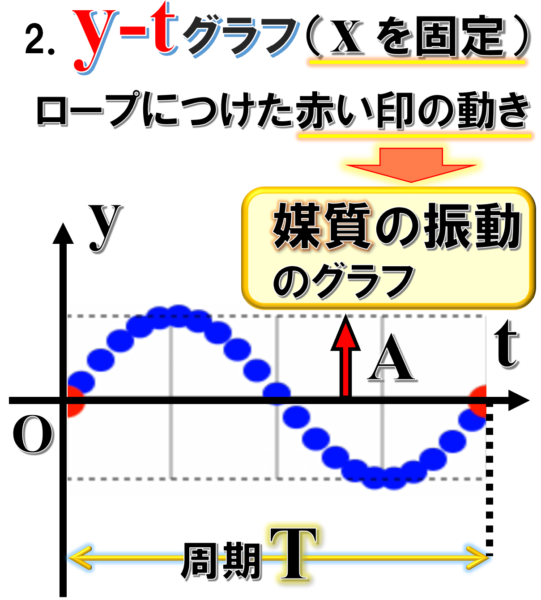

横軸がt はストップウォッチ(時間を測る)ですね。
ですから、この一つの波を作るのには1周期という時間がかかります。
これは波形ではありませんから気を付けてください。
それから、これは敢えて言う必要はないかもしれませんが…。

振幅は変わりません。
こうやって、波を表すことが出来るという訳です。
部屋の外の人に波を伝えるというのは、こんなことをしないといけないです。

写真を撮って伝えたりするわけですが、写真は動きが苦手なんです。
そこで、赤い印をつけて、印がどんな動きをしているかというところを見るんです。
そんな方法があるというわけです。

なかなか難しかったですねぇ…。
問題を解く時の注意事項

さぁ、それで次に3番へと進んでいきたいところなんですが、この2つを使ってお話をしていきたいことがあります。
実は。こちらのグラフを使った問題が、よく出題されるんです。

それはそうですよねぇ…。

見た目ですから…。
写真って手に入りやすいですものですから…。

だから、「こんな波がありましたよ!」っていう設定の問題がたくさんあるわけなんです。
その中で、実は写真というのは先ほどから何度も言ってきましたが、動きを見るのが非常に苦手なんです。
しかし、写真を使って、動きを見る方法があります。

さぁそれは、どんな方法だと思いますか?
写真を見て動きが分かる。例えば、スポーツ雑誌とか。
スポーツ記事とかにそれがあります。
例えば…

野球のスイングだったり、ゴルフのスイングだったり、
プロ野球選手がバットを構えて打つ。

プロゴルファーがドライバーを持って、パァ~んと打つ時があります。

そういう時に、ビデオとかテレビだったら、そのまま振っている所を写せばいいんですが…

これをスポーツ雑誌とか新聞に載せて伝えたい!
と思ったら…
パシャパシャパシャって撮った写真を並べればいいんです。

もうわかりましたね。

連射です。連射。
もう既に、波の問題を解いたことがある人だったらわかると思います。

何かグラフをちょっとずらすっていうような、そんなのを見たことがないでしょうか…?
問題集なんかでは、
これは覚えておくテクニックだよ!
とか書いてありますが…

全然、覚えることではありません。
写真なんです。
動きがわからないに決まっているんです。

でも、「写真から動きを言えと言われたらどうするか?」ということです。
だから、その時は連射すればいいんです。
もうちょっと時間が経った時のグラフを手に入れればいいんです。

今からやってみます。
今こういう状況です。
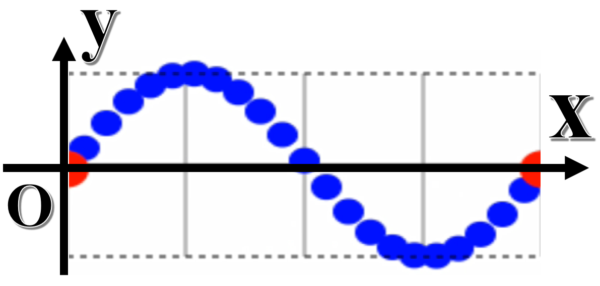

ちょっと時間が経ったらどうなるか?
ちょっと時間が経てば、こう移動します。
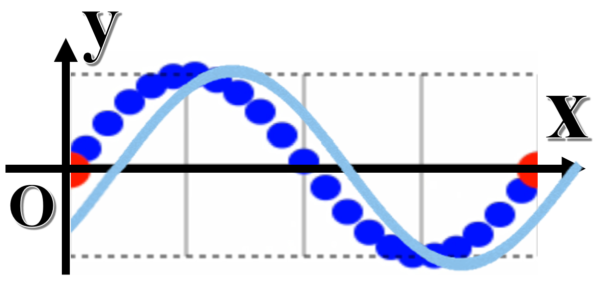
それでは、例えば、

ここにあった赤い印ってどこに行くと思いますか?
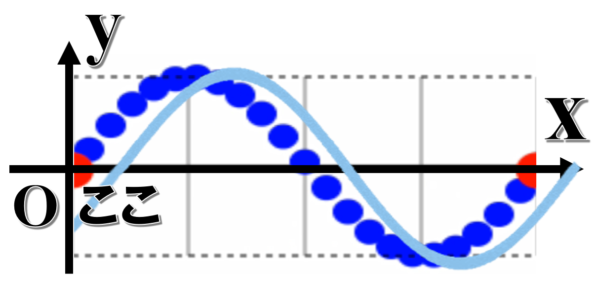
それは、ここに行きます。
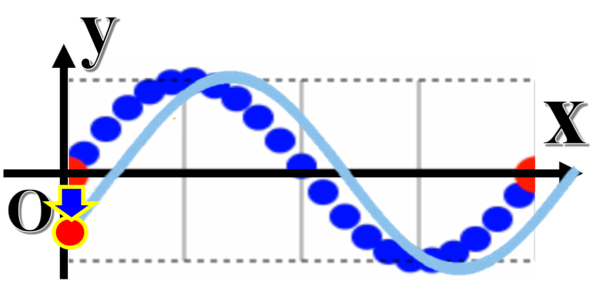
ここの印は、どこに行きますか?

それは、ここに行きました。
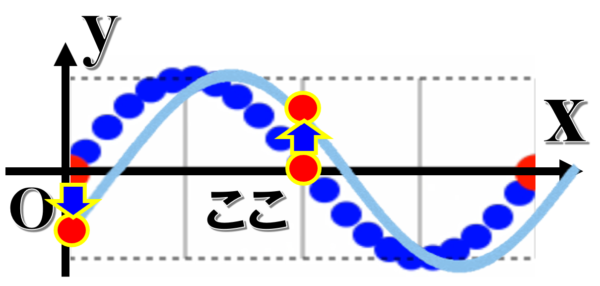

ほ~ら、動きがわかりました。
連射するだけで、動きがわかる。

それがすごいんです。
波のグラフをちょっとずらせば良い!
↑なんて覚えるという事ではないんです。
それでは今度はy-tグラフに行きます。
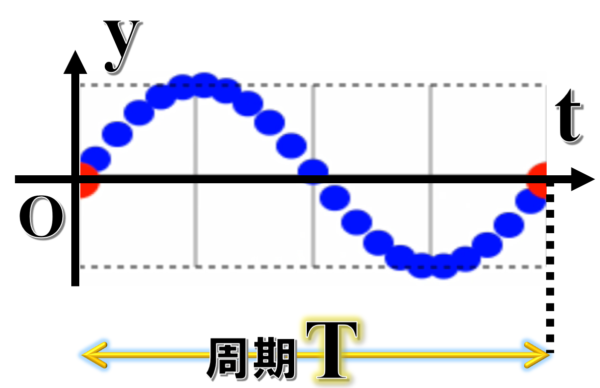
このグラフを動かす人がいるんです。

それダメです。
このグラフを動かしても何もわかりません。

動かすこと自体禁止です。動かしたって何1つわかりません。
これは、物理的意味を持ちません。
ところが、受験のテクニックとして、グラフをずらせばいいと覚えてしまう。
そんなことしたって、ずらせないんです。

なぜ?
ってことがわからないと、それは物理ではないんです。
ですから、
必ず何でずらせば良いのか?
一体いつずらすのか?
何が欲しい時にずらすのか?

だいたい1枚の写真しかないのに、動きが分かるのか?
って、頭の中で考えるんです。
すると、

そんなの無理だ!
って結論になる。

写真1枚で動きなんかわかるわけないじゃないか!?

その時は連射するんです。
これでy-xグラフ、y-tグラフについては終了しました。
次回は縦波の横波表示について解説します。