目次
はじめに
それでは浮力について見ていきます。
□下記は、分子レベルでみた浮力のイメージ動画です。
アルキメデスの原理
水や空気などの液体や気体のことを流体と呼ぶことがあります。

流体中に物体を入れると、入れる前に比べて物体は軽くなったように感じます。
例えば、ボールは空気中では手を離すと地面に落ちますが、水の中に入れると、ボールは浮かび上がります。


これは、流体から物体に重力とは反対向きの力がはたらくからです。
このような力を浮力といいます。
ボールが水面に浮かび上がるのは、ボールにはたらく下向きの力よりも上向きにはたらく浮力の方が大きくなるためです。

浮力の大きさについては、アルキメデスの原理が成り立ちます。
アルキメデスの原理とは、
流体中の物体は、それが排除している
流体の重さに等しい大きさの浮力を受ける。
という内容で、今から、これについてもう少し詳しく見ていきます。


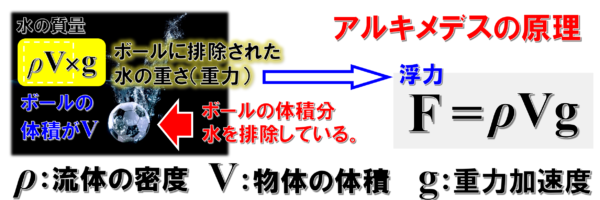
アルキメデスの原理によると、流体の密度をρ、物体の体積をV、重力加速度をgとすると、浮力の大きさは数式ではρVgと表現することが出来ます。
例えば、水中にあるボールの体積をVとします。

「それが排除している流体」とは、本来、流体が存在していたはずの所にボールがあるということです。
したがって、ボールが排除した体積はV
それに水の密度ρをかけると、それは水の質量になります。
さらに重力加速度をかけると、水の重力となります。

アルキメデスの原理によると、水の重力と同じ大きさの力を
浮力として上向きに受けるという訳です。
浮力の式の導出

浮力の式を物体にはたらく圧力の関係から説明すると次のようになります。
水中にある物体は、全方向から圧力を受けます。
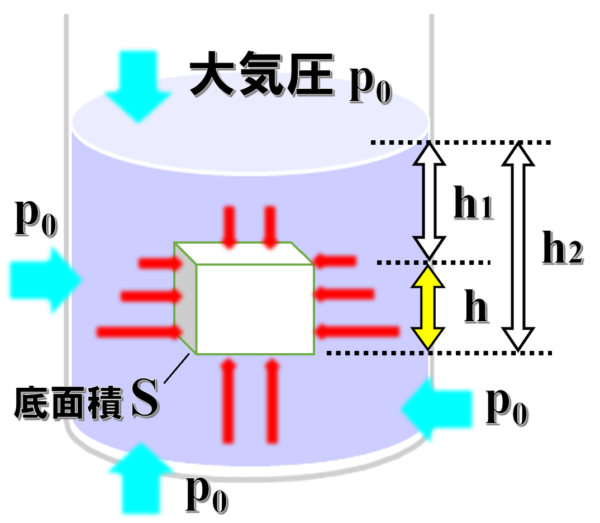
この圧力は、地球上の大気による圧力p0と水圧に由来します。

大気圧p0はほぼ一定ですが、水圧については前回解説したように水深によって決まる量です。
物体の上と下では、加わる水圧の大きさが違います。
側面が受ける力についても、水深が深くなるについて大きくなっていくので、これについては注意しないといけません。
まず、物体の側面にはたらく圧力から見ていきますが、ある高さにおける水圧は、反対側の水圧とつり合っているので、全体でみると力は互いに打ち消し合っています。
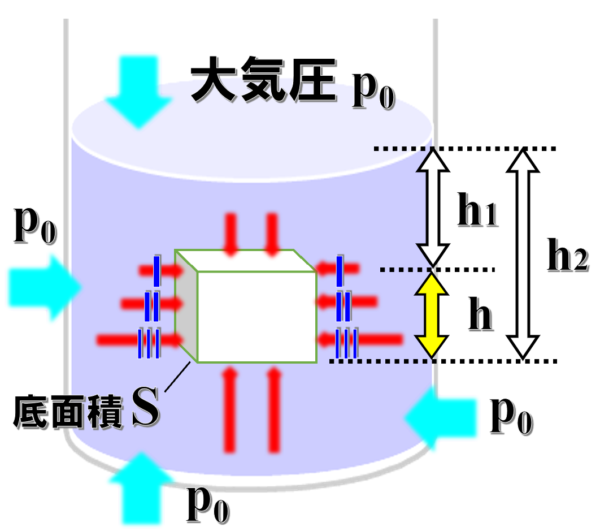
図で言うと、左側の圧力と右側の圧力がつり合いの関係にあります。

したがって、物体の側面については、トータルでは力がはたらいていないのと同じことになります。
次に、物体の上と下の方を見ていきますが、大気圧p0、水圧は水深h1[m]のところでは、ρh1gなので、物体の上からはたらく圧力は、p0+ρh1gとなります。
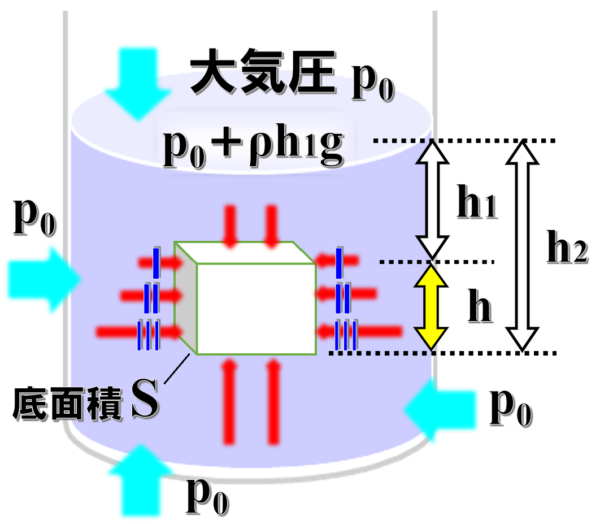
それに物体の底面積Sをかけて、上からはたらく力を求めて、これをF1とすると、F1=(p0+ρh1g)×Sとなります。
そして、物体の下からはたらく圧力は、水深h2[m]での水圧はρh2gとなるので、p0+ρh2g です。
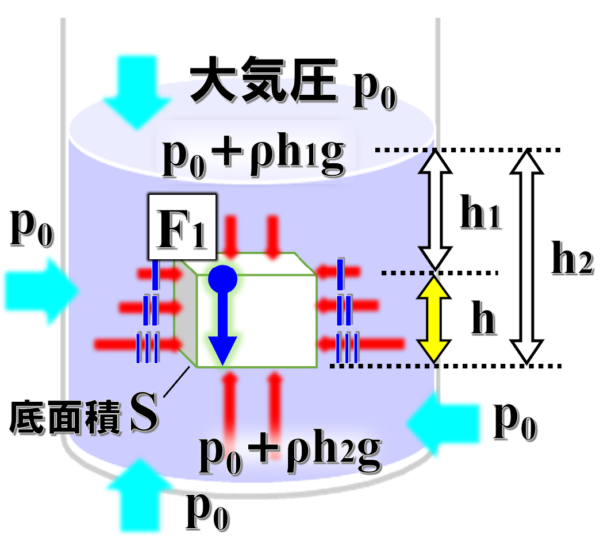
したがって、下からはたらく力をF2として、
F1と同じようにF2を求めると、F2=(p0+ρh2g)×Sとなります。
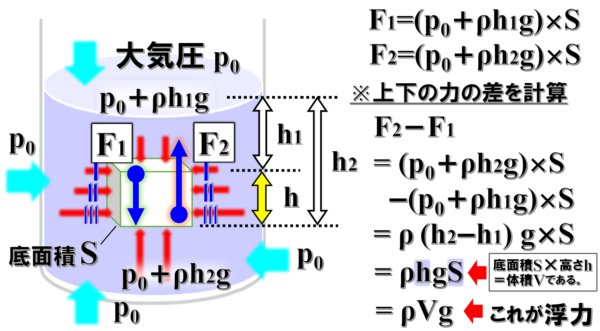
この時、物体にはたらく力の差を考えてみると、
F2-F1=(p0+ρh2g)×Sー(p0+ρh1g)×S
これを計算すると、ρ(h2-h1)gS
となって、h2-h1は物体の高さhと同じですから、これをhに置き換えると、
ρhgS
h×Sは、底面積×高さですから、これは物体の体積Vです。
したがって、最終的にF2-F1は、ρVgとなってアルキメデスの原理と同じ結果となります。

つまり、浮力という力は、物体の下からはたらく圧力と上からはたらく圧力の差によって生じる力だという事です。
練習問題
浮力という力は、流体の密度ρと流体の中に存在する物体の体積V、重力加速度gによってρVgと表現できることを確認したところで、1つ問題を解いてみます。
縦10cm、横10cm、高さ6.0cmの木片を水に浮かべると、4.0cm沈んだところで木片は静止した。水の密度を1.0×103kg/㎥とし、重力加速度の大きさを9.8m/s2とする。
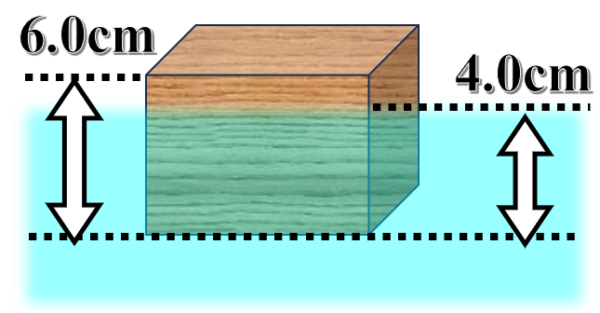
(1)水に浸かっている部分の木片の体積を求めよ。
木片は4cm浸かっているので、高さは4cmで計算します。
この後、水の重さや質量を計算しないといけないので、メートル単位に直してから体積を計算すると、
縦、横、それぞれ0.10m×高さは0.04で、木片の体積は、4.0×10-3となります。
![]()
(2)木片が排除した水の重さ(重力)を求めよ。
木片が排除した水の質量は、密度×体積から求めると、密度は、1.0×103×体積は4.0×10-3
これを計算すると水の質量は、0.40kgとなって、それに重力加速度をかけると、水の重さは3.9Nになります。

(3)木片が受ける浮力の大きさは何Nか。
アルキメデスの原理によると、木片が排除した水の重さと同じ大きさの浮力を受けるので、木片が受ける浮力の大きさは3.9Nになります。
![]()
(4)木片の質量は何kgか。
木片の質量をmとすると、木片にはたらく重力と浮力がつり合っているので、力のつり合いの関係から、木片にはたらく重力は、m×9.8
それが木片が受ける浮力に等しいという式を立てて、mを計算すると、mは0.40kgとなります。

ここの計算では、水の重さを計算する時の0.40×9.8の計算式を使っているので注意してください。
それでは、今回の解説は以上となります。