
はじめに
今回は、力のモーメントと剛体のつり合いということで、講義を進めていきます。
前回の講義では、力のつり合いについて学習しました。
■動画での解説はこちらをチェック
1.剛体とは

静止している物体にはたらく力がつり合っていれば、その物体は静止したままである。
ということをお伝えしましたが、実は、これは特別な場合にのみ成り立つ現象なんです。

つまり、必ずしも「力がつり合っていれば物体は静止している」というわけではないということです。
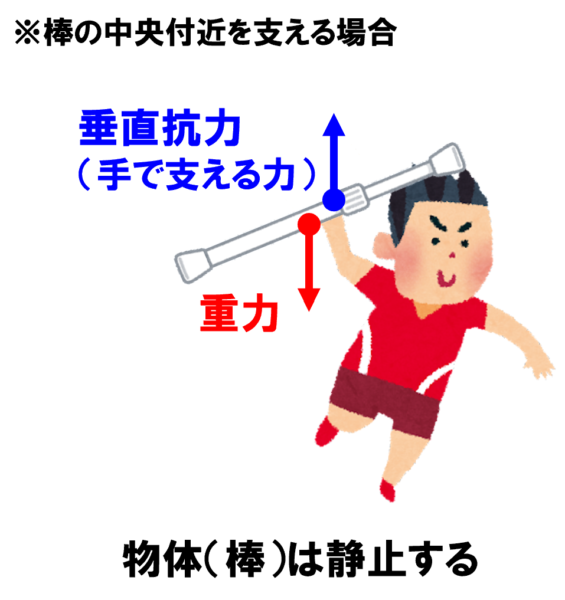
たとえば、次の図のように下向きの重力とつり合うように下から手で支えているとします。

この状態だと物体は静止しています。

しかし、この物体が形を変えて、棒状になったらどうですか?


下向きの重力とつり合うように端っこを持ったらどうなるか?
端っこを支点にしてくるっと回転します。

この棒の真ん中あたりを持てば、力はつり合って静止します。

今示したように、物には必ず「大きさ」というものが存在していて、同じ向きで同じ大きさの力であっても、物体のどこから作用させるかによって結果が変わってくるわけです。
前回の講義では、物体の大きさを考えなくてもよいという前提で話を進めていました。
物理では、
質点:物体の大きさを考慮しなくてもいい理想的な物体
剛体:どんなに力を加えても形が変わらない物体
と言います。
今回の講義では、剛体がつり合う条件について考えていきます。
2. 力のモーメント
今から剛体がつり合う条件について考えていくわけですが、そのために力のモーメントという概念を理解しておかなければいけません。

とは言っても、いきなり力のモーメントの説明を始めても難しいので、簡単なものというか身近なものからだんだん近づけていこうと思います。
ここにシーソーがあります。

このシーソーにお父さんとその子ども乗っかるとします。

支点の位置が真ん中だとお父さんが下にさがっていくのが目に見えているので、支点をお父さんの方にずらします。

そうすると、シーソーのバランスが取れて、どちらにも下がることなく静止しました。
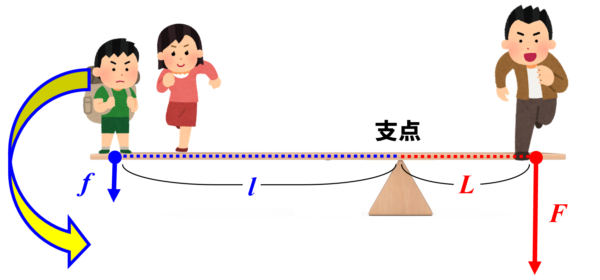
この時、お父さんにはたらく重力をF、子どもにはたらく重力f、支点からの長さは、お父さんの方をスモールl、子どもの方をLとします。


そうした時に、「シーソーがつり合っている」ということを数式で表現するにはどうしたらいいか?
重力の大きさだけを比べるとお父さんの方が大きいですから、力だけでは不十分です。
しかし、何となくですが、
F ×l=f× L
としたら説明できそうです。

結論から言うと、それでいいのですが、それでは 「F×lというのは何なのか?」という事を考えないといけません。
それで、バランスの取れた状態から、例えば子どもの方にお母さんが乗っかったら、シーソーは時計回りに回転しそうですね。
逆に、支点を中央に移動させたら、シーソーは反時計回りに回転するでしょう。

そのように考えていくと、このF×lというのは、「回転の能力」を表しているということが見えてきます。

このような物体をある支点のまわりに回転させようとする力の作用のことを「力のモーメント」と言います。
ここで整理しておくと、力のモーメントの大きさは、力の大きさ×うでの長さ で与えられます。うでの長さというのは、シーソーで言うと、支点の位置からお父さんの位置、つまり、力の作用点までの距離のことです。
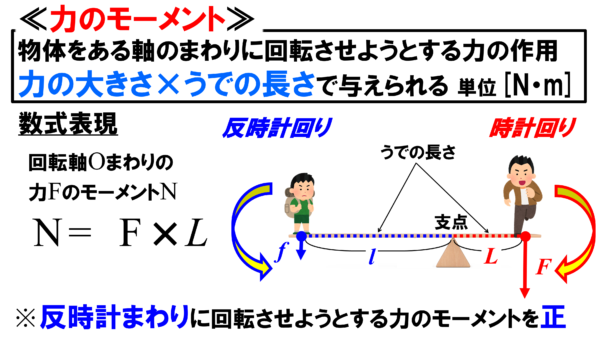
注意しないといけないのは、うでの長さは、力の作用線に下ろした垂線の長さであるということです。シーソーの場合であれば、支点の位置からお父さんに位置までがそのまま腕の長さになりました。
こちらの図の場合であれば、腕の長さは、回転軸から力がはたらく方向に引いた線に下ろした垂線の長さになります。
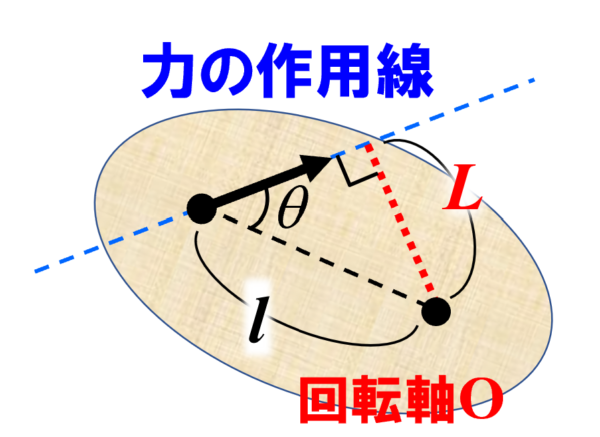
したがって、図の場合だと、回転軸Oまわりの力FのモーメントNは、N=-Flsinq となります。

3.剛体のつり合い
力のモーメントについて確認したので、ここで剛体がつり合う条件について考えていきます。
剛体がつり合っているというのは、剛体が前後に進んだり回転しない状態を指します。
前に進んだり回転しない時に、剛体は静止しているというわけです。
したがって、剛体がつり合う条件は次のようになります。

次の記事では実際に問題を解いていきます。
















