
目次
はじめに
前回の記事で「力のつり合い」の基本事項を確認したので、実際に問題を解いていきます。
■前回の記事
力のつり合いの問題
重力加速度の大きさを9.8m/s2として、以下の問いに答えよ。
問1.解説
問1.ばね定数7.0×102N/m(ニュートン毎メートル)のばねの一端を天井に固定し、下端に質量5.0kgのおもりをつるして静止させる。このときのばねの伸びを求めよ。
力の単位にはNと書いて(ニュートン)という単位を使用します。この辺りについては、5回目の講義で詳しく学習します。
5.0[kg]のおもりには下向きの重力が働いていて、その大きさは、5.0×9.8 = 49[N]になります。このおもりはばねに繋がれていて、ばねの伸びをx[m]とすると、弾性力の大きさは、(7.0×102)×x[N]となります。
おもりは静止しているわけですから、この2つの力はつり合っています。
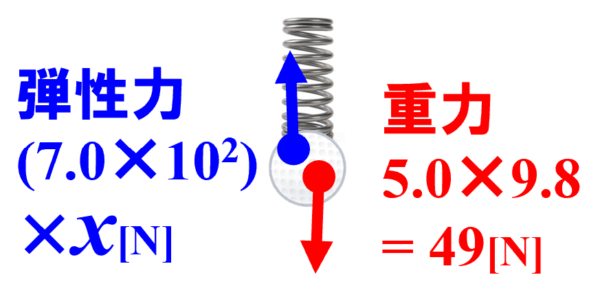
したがって、(7.0×102)×x = 5.0×9.8 という式が成り立ちます。ここからxを求めると、x=0.07[m]ということで、この時のばねの伸びは0.07mとなります。

問2.解説
問2.問1のおもりをばねのかわりに糸をつかってつるし静止させる。このときの糸の張力の大きさを求めよ。
糸の張力の大きさをT[N]として、このTがいくらなのかを求めていきます。おもりにはたらく重力は下向きに49[N]で、これをばねに代わって糸が引っ張って支えるというわけですから、糸が引っ張る力、つまり糸の張力は49[N]となります。

問3.解説
問3.つぎに、おもりに別の糸をつけて水平方向に引き、おもりをつるしている糸が鉛直方向と30°の角をなすように静止させる。2つの糸の張力の大きさを求めよ。
少し複雑な問題なので、図に書いて整理していきます。上から糸でつるされた重りに、別の糸をつけて水平方向に引っ張る。そうすると、鉛直方向と30°の角度を成すように静止するわけです。
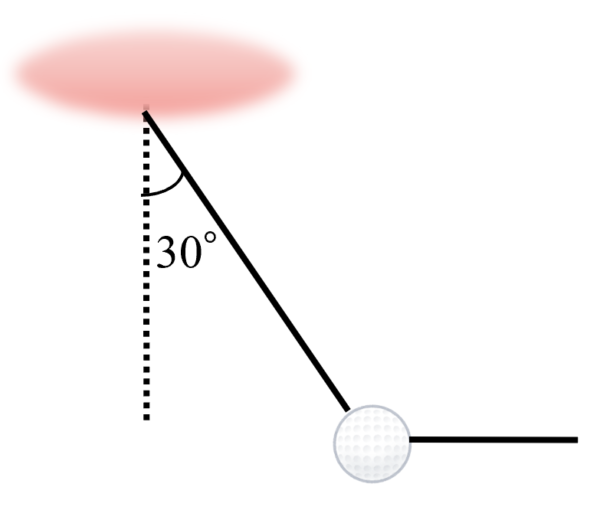
おもりにはたらく重力は49[N]で、天井からつるされている糸の張力をT、水平方向に引く糸の張力をSとする時に、TとSを求めるのが、この問題の問いになるわけです。

おもりが静止しているわけですから、この3つの力がつり合っていることを利用すれば良いわけです。

しかし、そのままではうまく行きません。
そこで、この斜めにはたらく糸の張力Tを2つの方向に分けてみます。これを力の分解といいます。

今から、力の合成とは逆のことをやってみようという訳です。
それで、この糸の張力を水平方向と鉛直方向に分解をします。そうすると、鉛直方向の力はTcos30°、水平方向はTsin30°となります。


これは、三平方の定理でやりましたね。1:2:√3の関係です。
こうすると、おもりが静止しているのは、水平方向の2つの力と鉛直方向の2つの力がつり合っているからだという事が見えてきます。
これを順番に数式で表現すると、
水平方向の力のつり合いから、S = Tsin30°
鉛直方向の力のつり合いから、Tcos30°= 49
この2つの式を連立して解くと、T≒57[N]、S≒28[N]となります。

問題演習
例題に続けていくつか問題を解いていきます。
(1)解説
(1)あらい水平面上に質量10kgの物体を置く。物体が面から受ける垂直抗力の大きさを求めよ。
質量10[kg]の物体には下向きに重力が働きます。そして、あらい水平面上に置かれて静止しているので上向きに垂直抗力が働いており、この二つの力がつり合っていることが分かります。

したがって、垂直抗力の大きさをN1とすると、N1=98で垂直抗力は98[N]となりま。

(2)解説
(2)(1)の状態から物体に糸をつけ、鉛直上向きに60[N]の力で引いたところ、 物体は動かなかった。物体にはたらく垂直抗力の大きさを求めよ。
物体には下向きに98[N]の重力が加わり、上向きに60[N]の糸の張力、そして垂直抗力が働いて静止しています。
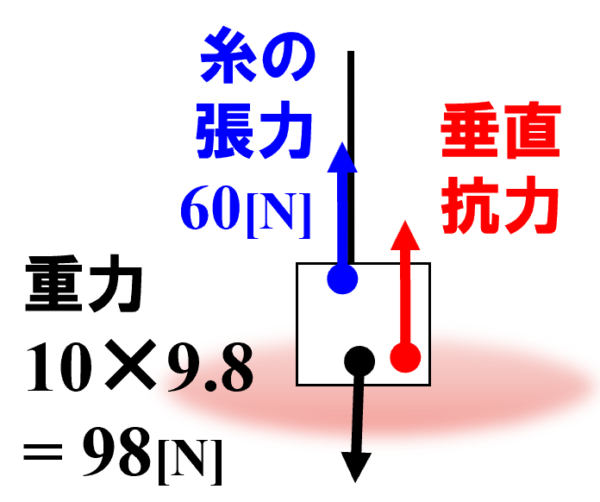
この時の垂直抗力の大きさをN2とすると、力がつり合っていることから、
N2+60=98
したがって垂直抗力は38[N]となります。
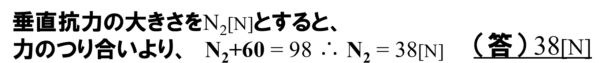
(3)解説
(3) つぎに糸を物体の側面につけ、水平方向に30[N]の力で引いたところ物体は動かなかった。物体にはたらく摩擦力の大きさを求めよ。
今度は物体の側面に糸をつけて30[N]の力で引いたわけですが物体は動きません。このとき、物体の水平方向の動きを妨げるように摩擦力が作用していることから、摩擦力の大きさをF1とすると、力のつり合いの関係より、F1は30[N]となります。

(4)解説
(1)の状態から物体に糸をつけ、水平方向から30°上方に30[N]の力で引いたところ、物体は動かなかった。物体にはたらく垂直抗力の大きさを求めよ。
物体に働く力を確認していくとまず場の力である重力。
接触力は垂直抗力と糸の張力。そして、糸に惹かれまいとあらい面から働く摩擦力の以上となります。
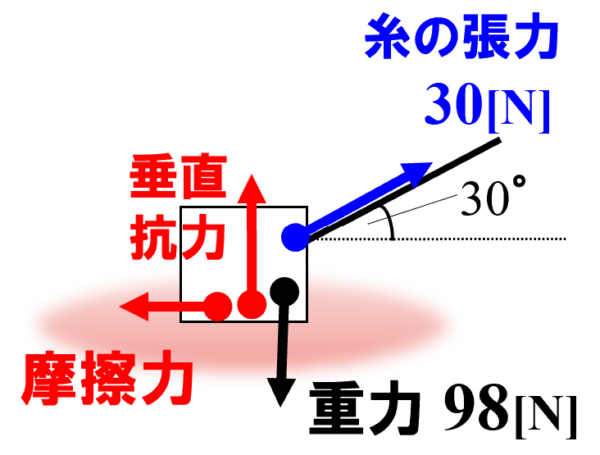
このとき、図のように糸の張力を鉛直方向と水平方向に分解して力のつり合いを考えていきます。

まずは垂直抗力の大きさをN3とすると、鉛直方向の力のつり合いの関係から、
![]()
が成立します。これより、N3=83[N]となります。
(5)解説
(5)(4)のとき、物体にはたらく摩擦力の大きさを求めよ。
摩擦力は、水平方向の力の釣り合いの関係から求められます。摩擦力の大きさをF2とすると、
![]()
これを計算すると摩擦力の大きさは、26[N]となります。

これですべての問題の解説は終わりました。
今回の講義から高校物理力学の内容はより深みを増してきますので、一つ一つの定義をきちんと押さえながら学習を進めてください。
力の定義、そして場の力と接触力。慣性の法則と作用反作用の法則。どれもこの先の学習内容と大きく関わってくる事柄になってきますので、きちんと理解できるようになってください。
それでは今回の授業はここまでとなります。お疲れさまでした。















