はじめに
今回は回路のまつわる例題を解説していきます。

題材として取り扱うのは、重要問題集115のコンデンサーを含む直流回路の問題です。
※問題文を掲載すると著作権に抵触するため、重要問題集をお持ちでない方は書店等でお買い求めください。
回路の問題に対する対処方法については、前回の講義で合成公式を導く課程の中で確認してきました。
□前回の講義
その中で、如何に基本式を大切にするか。電位の関係式(=キルヒホッフの第2法則)をどのように使っていくか。
更にその前のクーロンの法則の講義では、
電位というのはプラス1クーロンあたりの位置エネルギーである!
ことを学んできました。

回路の中にプラス1クーロンの電荷を持ってきて、「それが電気的にどれだけ高い位置にいるか?」ということを考えると、電位の関係式を容易に立てられる。

コンデンサーであったり抵抗に高低差をつけているのは、電荷を組み上げるポンプの役割である電池である。
といったことを解説してきました。
キルヒホッフの第2法則を学んだ人は、回路を回りながら上がるとか下がるとか、そういうことを言いながら足したり引いたりしてきたと思いますが、

結局あれはプラス1クーロンを持って回路の中を回っているわけです。
そのように高いところにいったり低いところにいったりという
回路の中にあるプラス1クーロンというもののイメージを正しく持つことがとても大切。

電位の式は非常に大事な式です。
それが正確に立てられないと、連立方程式を解いても間違った答えになってしまいますから、慎重に立てていかなければいけません。
コンデンサー回路のスイッチ操作(前編)
これから問題を解いていくわけですが、一番大事なのは電位の関係式です。電位の関係式というのは、1クーロンあたりの位置エネルギーの話です。


位置エネルギーは、電気的な高さ。
今、電気的な高さを与えてくれるのは電源です。
今からこの回路を問題の設定と矛盾しないように書き換えてみようと思います。
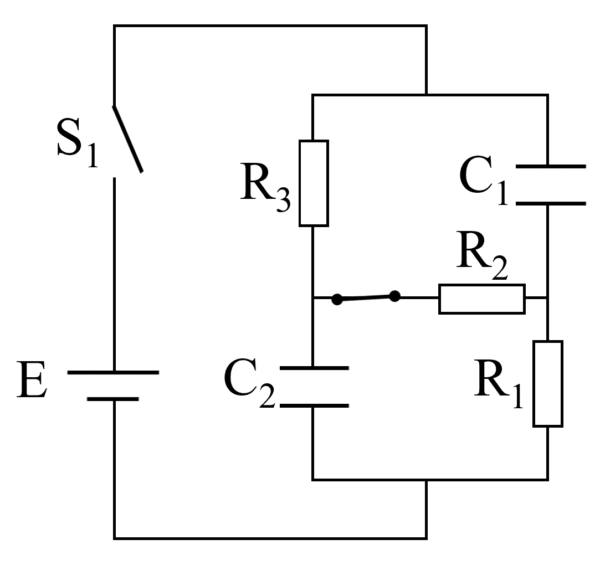

起こすというのは、電池とか抵抗を横向きから縦向きにするということです。
R2だけ横向きになってしまいましたが、全体的に横方向から縦方向の向きに変わりました。

なんでこんなことしたの?
という話なんですが、

こうしておくと電位の関係式を作る時に便利になります。

これくらいならできる!
って人もいるかもしれませんが、

回路の問題に苦手意識を持っている人は、こうして書き直す癖をつけておくと良いと思います。
ただし、回路図は定規で書かないことをお勧めします。
試験中に律儀に定規で回路図を書いていたら試験時間がなくなってしまうので、フリーハンドで書くようにしてください。

それでは解答に移っていきます。
(1)解説
(1)S1を閉じた瞬間にR2を流れる電流はいくらか。
前置きの話
こういう回路を見た時に合成しようとする人がいます。
しかし、それは出来ません。

CとRは合成できないですからね。
V=IR、Q=CVをそれぞれについて述べていかないといけません。

これから実際に電位の式を立てて問題を解いていくわけですが、この問題の問いを見た瞬間に、解答がパッと閃いた人にとっては、この先の解説を煩わしく感じるかもしれません。
というのも、重要問題集の解答にある通り、電流は流れやすいところに真っ先に流れ込むわけですから、S1を閉じた瞬間は抵抗を避けてコンデンサーの方に流れ込みます。

次の(2)番では逆に、充電完了したコンデンサーには、これ以上電荷は蓄えられないわけですから、電流は流れない。


しかし、そういう解き方しか知らない人は、(4)の問題で行き詰まってしまいます。次の(5)は、(4)と連動しているので、(4)が得点出来なかったら、(5)も得点出来ません。

そもそも、このような解き方というか、重要問題集の解答にあるような、「スイッチを閉じた瞬間のコンデンサーは導線と同じ!」なんて考え方は学問としての物理ではありません。
コンデンサーは導線ではありません。2枚の鉄板が少しだけ距離をあけて置いてあるだけなんです。

たとえ導線と同じだと思えば問題が解けるにしても、それでは本当の物理の実力は身につきません。

それじゃあ仮に、導線と仮定したC1を電流が通過したときに、なんでR1とR2に電流は分岐しないんですか??

そうやって聞かれたらどうするんですか??

R1を通ろうが、R2を通ろうが、同じ電気抵抗を1箇所通過したことに変わりないじゃないか??

しかもR1の方が抵抗が小さいから、むしろR1に流れるはずじゃないか??
やはり、そういった疑問を解消していくためにも、問題を解く時にはきちんとした手順で問題に向き合っていかなければいけません。

皆さんは決して、この問題の解き方を覚えるために問題集を解いてるわけじゃないはずです。
問題演習を通して、見たことがない入試問題を解くための実力をつけるためにやっているんです。
解説

これから電位の式を立てていくわけですが、それぞれの部品に対して、V=IR、Q=CVを立てないといけないので、抵抗を流れる電流とコンデンサーに蓄えられている電荷を仮定しないといけません。


そうしたら実際に電位の式を立てていくわけですが、よく回路を見て下さい。
今、プラス1クーロンを回路に持ってきた時に、1クーロンの電荷には、R1方向へ行く道とC2方向へ行く道があって、さらにC2を登った後には、R3方向へ行く道、そして遠回りになるけどR2を通ってC1方向へ行く道があります。
そして、R1を登った後は、C1方向へ行く道とR2を経由してR3方向へ行く道があります。

したがって、電位の式は合計4通り立てられることになります。
まずは、C2を登ってR3を超える式です。

プラス1クーロンの電荷がC2分のq2だけ、タッタカタッタカ登って、「あぁしんどいなぁ…」、さらにi3R3だけ登って「あぁしんどかったぁ…」。こんな高低差をつけたのは誰??
って、
あんた

あんた(電池E)だね!
ということで、1つ目の式は出来ました。
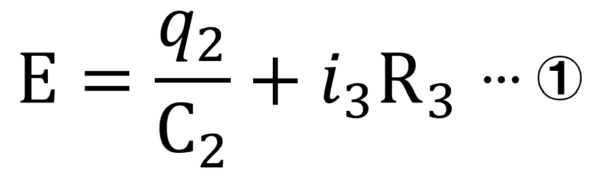
それが①の式です。
それでは続けて同じように残りの3つの式も立てていきます。

今度は、i1R1をタッタカタッタカ登って、あぁしんどかった。さらにC1分のq1登った。こんな高低差を作ったのはもちろんこの電池の仕業です。
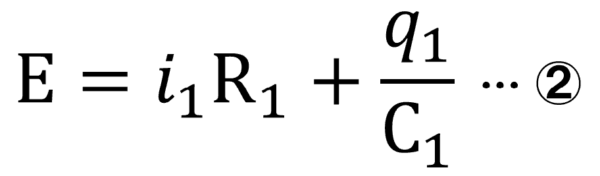

プラス1クーロンの電荷がC2を登ります。そして、遠回りになるけどi2R2を超えて、C1分のq1高いところにいったぁ~。
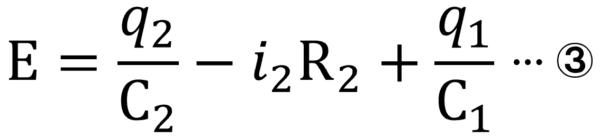
i2R2にマイナスが付いてますが、①式②式では矢印の反対方向を正としてました。それに対して、ここでは矢印に沿った方向を進んでいるので、向きが反対ということでマイナスをつけています。

最後に、i1R1を登って、i2R2に寄り道して、i3R3をタッタカタッタカ登って、あぁしんどかったぁ…。
![]()

これで解答の準備が出来たわけですが、まだこの式は解けません。

今、この式4つに対して、仮定した未知数の数は5つでした。

5つのものを仮定したにも関わらず4つしか式を立てられない…

題位とは…??

先ほど読み上げた問題文に何て書いてありましたか??
スイッチを入れた瞬間。

ということは、
Q=0です。

何でこういう所、上手く気付くんですか?
問題集の解答には、スイッチを入れた瞬間、導体の様になると書いてありました。

しかし、そうはなりません。
コンデンサーは鉄板が2枚重なってるだけですから。

だから q1 ここが0。
それだけのことです。

もしも電荷が与えられているなら、この式(①~④)を解いていけば良いんです。
その時は、qが与えられているはずですから…。

しかし、問題文には「コンデンサーに電荷が蓄えられていない。」とは書かれていないので、この問題を解答する時は、そういう前置きをしておいた方がいいですねぇ…。
つまり、
初めコンデンサーには電荷が蓄えられていなかったとすると、題位よりq1=0、q2=0
と、記述式の問題であれば一言、断りを入れておきます。
![]()
従って、③式からi2を求めると、S2の向きに3Aの電流が流れることがわかります。
i2は−3 ですから、最初に仮定した向きとは逆向きに電流が流れるという事です。
電位の式を立てる時に、③式と④式では電流の流れる方向が逆向きになってましたよね。きちんと電位の式を立てて電流を求めると、流れる方向も正負の符号付きできちんと決まります。
(2)解説
(1)では、抵抗やコンデンサーの数だけ基本式を考え、電位の式を立てて実際の問題を解いていきました。

なぜだかわかりますか??


回路が変わらない以上、最初に立てた式はずっと使えるんです。
(2)番は、(1)と同じくR2を流れる電流を求めないといけません。
ということは先ほどと同様、仮定したものが5つなのに対して式は4つですから、

必ず題位から何か1つが決まります。
問題文には、十分時間が経ったとあります。

十分時間が経ったということは、コンデンサーの充電が完了したということですね。
それなら、はっきりと「コンデンサーの充電が完了したときのR2を流れる電流はいくらか?」って聞いてくれた方がわかりやすいのですが、入試問題は受験生を選抜するための問題なのでこういう意地悪なところがあります。

だから、少しずつこういった入試問題特有の言い回しには慣れていってください。
さて、それでは解答に入っていきますが、コンデンサーの充電が完了したということは、
コンデンサーにこれ以上電荷は流れ込まない!

断線した訳じゃないですからね。
電流が流れると断線する回路なんて…
不良品じゃないんですから。

言ってしまえば、そもそもコンデンサーは2枚鉄板を重ねただけですから、もともと断線してるというか繋がってません。

ということは、プラス1クーロンの電荷にとってみれば、

C2とR1の分岐点があって、C2は行き止まりだから、R1を登ろう!

あぁ…高いところに行ったぁ。
次も分岐点だ!

だからR2を経由してからR3を登ろう!


それ誰のせいって…、あんただね。
要するに、電流は抵抗R1, R2, R3だけしか流れないというです。

(3)解説
(2)のとき、C1に蓄えられた電荷はいくらか。
直列とか並列とか言ってる人は、

ってパニックになるでしょうねぇ…。

こういったところで、「ごまかさずに勉強してきたかどうか?」という所の差がはっきりと現れてきます。

コンデンスされて電荷が濃縮されたから、これ以降コンデンサーには電荷が入り込まない!
って、言ってるだけですから、コンデンサーには電荷が存在します。
だから電気的な高低差は当然存在します。

したがって(1)で立てた、①~④の電位の式は全て使えます。

ここでは、②の方が計算が簡単なんでこれを使いましょう。
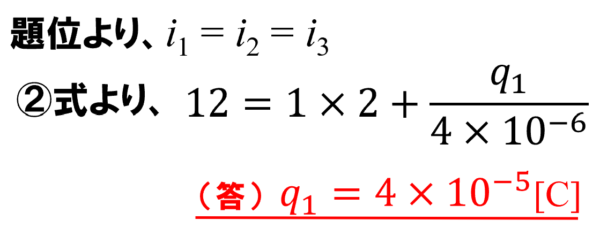

どうですか。実際に問題を解いて見て。
電位の式を立ててしまえば、後は問題文が与える条件に沿って解いていけば良いということがわかって頂けたと思います。
■回路の問題解法②(制作中)



















