はじめに
それでは、今から実際に万有引力にまつわる問題を解いていきます。
□万有引力の復習はこちらを参照してください↓↓
今回取り扱う問題は、重要問題集の49番、ケプラーの法則の問題です。
※問題文を掲載すると著作権に抵触するため、重要問題集をお持ちでない方は書店等でお買い求めください。
重要問題集の49番、ケプラーの法則

地球の自転と公転を無視するということは、地球上の万有引力を重力と同等に扱ってもよさそうですねぇ…
それでは問題に移ります。
(1)解説
(1)地球上での重力加速度の大きさgを、R、M、Gを用いて表せ。
何も知らない状態で、この問題を見たら、gをRとMとGで表せと言われても、何から手をつければいいのかわからなくなりそうですが、これは3つのポイントでやりました。

それで実際にG、R、Mを入れて計算してみると、ちゃんとgが9.8になってましたね。

実際の重力加速度は、地球の自転などの影響で少し小さくなりますが…??

問題文では地球の自転と公転を無視するということですから、これでいいでしょう。
ということで、
gは次のようになります。


問題文には、単位が添えられているので、解答にも忘れずに単位をつけておきましょう。
(2)解説
それでは次の問題に移ります。
(2)物体の速度が地球の中心Oから2Rの距離にある点Aで0になるためには、初速度の大きさv0[m/s]をどれだけにすればよいか、g、Rを用いて表せ。
地球の上にある物体が、中心から2Rの距離まで打ち上げられて、そこで静止するというわけです。まっすぐに打ち上げて止まったわけですから、これは当然円軌道ではありません。
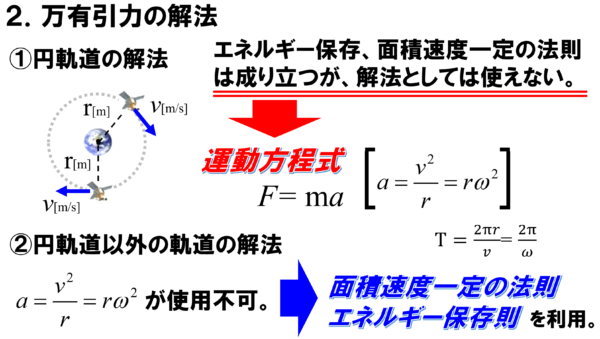

そこで、円軌道以外の解法を考えることにして、まずはエネルギー保存則から考えてみます。
そうすると、
物体は最初とても大きな負の位置エネルギー持っていたが、運動エネルギーを与えることによって、少しだけ負の位置エネルギーが小さくなった。
という式が立てられますね。
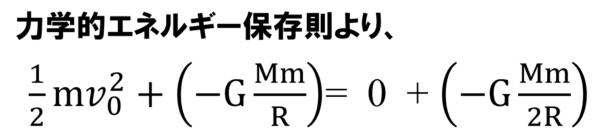
これを計算すると、
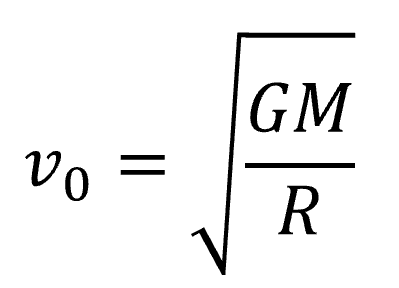
となって、gとRを用いて表せとありますから、(1)の結果を代入すると答え次のようになります。
![]()

ちゃんとgとRで表せていますねぇ。
(3)解説
それでは次の問題に行きます。
物体の速度が点Aで0になった瞬間、物体に大きさv[m/s]でOAに垂直な方向の速度を与える。
(3)物体が地球の中心Oを中心とする等速円運動をするためには、vをどれだけにすればよいか、g、Rを用いて表せ。また、この円運動の周期をg、Rを用いて表せ。

それから、物体はOを中心とする等速円運動をするわけですが、円運動は中心に落ち込む運動です。この時、物体を地球の中心に引っ張っているのは、地球からの受ける万有引力ですから、ここで運動方程式を立ててみます。

質量mの物体に、地球の中心に落ち込む加速度を与えたのは、地球からの万有引力である。そして、物体は等速円運動するので、次のように表現できます。

ここからvを求めることができます。答えはgとRを用いて表さないといけないので、これも(1)の答えを利用して、計算するとこうなります。
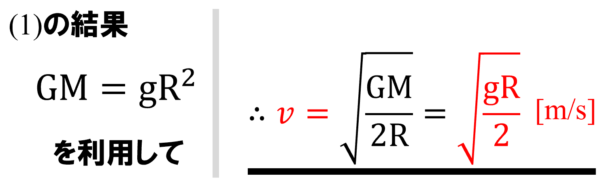

周期は、グルっと1周するのにかかる時間ですから、円周の長さを速さで割ってやればいいわけですね。
グルっと1周は2π×2Rで速さvは先ほど求めたやつも使えばいいので、周期Tは、次のようになります。 
(4)解説
さぁ、それでは次の問題に進んでいきます。
点Aで物体に与える速さvが(3)で求めた値からずれると、物体の軌道は、地球の中心を1つの焦点とするだ円となる。だ円軌道はvが大きくなるほど大きくなり、vがある値以上になると、物体は無限遠方に飛び去ってしまう。
(4)物体がABを長軸とするだ円軌道を描くとき、次の問いに答えよ。ただし、点Bの地球の中心からの距離は6Rである。
(a)点Aにおける面積速度と点Bにおける面積速度が等しいことから、点Bにおける物体の速さV[m/s]をvを使って表せ。
物体がだ円軌道に移ったわけですから、ここからは円軌道以外の解法を考えていきます。まずは、問題文にある通り面積速度一定の法則より、点Aと点Bにおける物体の速さの関係は次のように表現出来て、ここからvが求められます。
![]()
(b)速さvをg、Rを用いて表せ。
これから速さについて考えないといけないので、エネルギー保存則を立てていきます。

円軌道だったら運動方程式ですが、だ円軌道なので、ここはエネルギー保存則です。
こうして、万有引力の問題の解法を理屈として知っておくと、どの式を立てていけば良いのかという解法に迷うことがありません。
この時の点A、点Bにおける力学的エネルギー保存則は、次のように書けます。

この式に先ほど(a)で求めたVと(1)の結果を代入すると次のようになります。
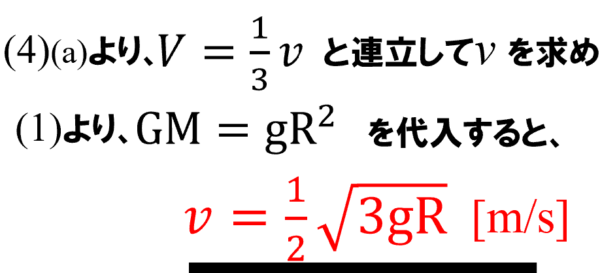
(c)このだ円軌道の周期をg、Rを用いて表せ。
だ円軌道の周期を求めるわけですが、ここでは等速円運動のように、円周割る速さで周期を求めることが出来ません。

ここではケプラーの第3法則を利用します。
ケプラーの第3法則は、惑星の公転周期の2乗とだ円軌道の長半径の3乗の比は、すべての惑星で一定になるという法則です。
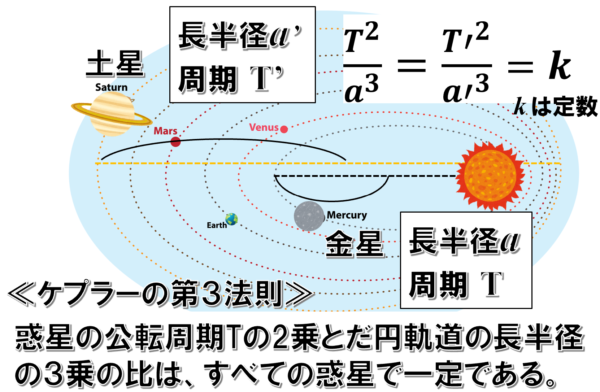
ケプラーは太陽系の惑星、つまり太陽の周りを公転する火星や木星などの惑星の観測データから導き出したわけですが、この法則は地球の周りを公転する月などの衛星についても同様に適用できることがわかっています。
ケプラーの第3法則をこの問題に当てはめて考えてみると、地球の回りを等速円運動する物体の周期Tの2乗と半径Rの3乗の比は、だ円軌道をする物体の周期の2乗と長半径4Rの3乗の比に等しくなるというわけです。長半径というのは、長径の半分なので、2足す6の長径8Rの半分ということで4Rです。
そこで、求める周期をT‘として式を立ててみると、次のような式となります。

これを計算すると、
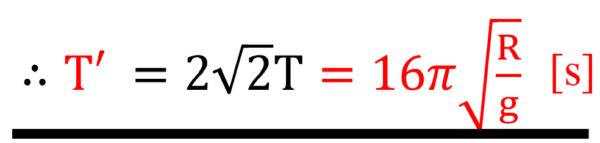
となります。
(5)解説
それでは、最後の問題です。
(5)物体が地球に衝突もせずかつ無限遠方に飛び去ることもなくだ円軌道を描き続けるためには、速さvはどのような範囲になければならないか、不等式で表せ。
この問題では、物体が無限遠方に飛び去らない速さvの条件とだ円軌道を飛行するための最小の速さvのそれぞれについて考えなければなりません。
まずは、無限遠方に飛び去らない速さvの条件ですが…

これは第2宇宙速度のところでもやりました。
大きな負の位置エネルギーを持つ物体に運動エネルギーを与えた時に、その力学的エネルギーが0になると物体は無限遠方で静止するわけですから、これより小さい速さであればよいわけです。

ということで、無限遠方で静止する速さをエネルギー保存則から求めてみます。
すると、点Aにおける負の位置エネルギーと運動エネルギーのトータルが0であるという式は次のようになります。
![]()
これよりvを求めます。
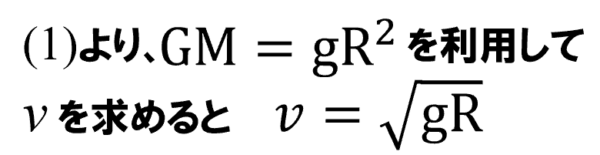

これで物体の速さがルートgRより小さければ、無限遠方には飛び去らないことがわかりました。
それからだ円軌道を描き続けるための速さですが、ここは間違えやすいのでよく注意をしてください。速さが遅くなっていくと、だ円の軌道半径がだんだんだんだん小さくなっていくわけですが、半径2Rの円軌道が最小の速さではありません。
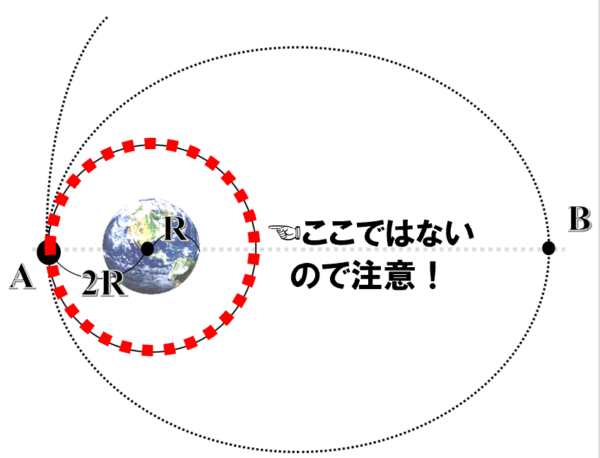
地球すれすれのだ円軌道を描くことも考えられますから、図で示した赤いだ円軌道について考えなければなりません。
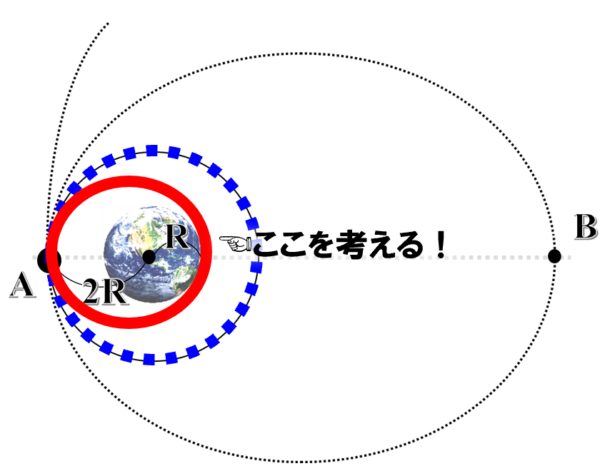
そこで、点Aでの速さをスモールv0、点Cでの速さをV0とした時のv0をこれから求めていきます。
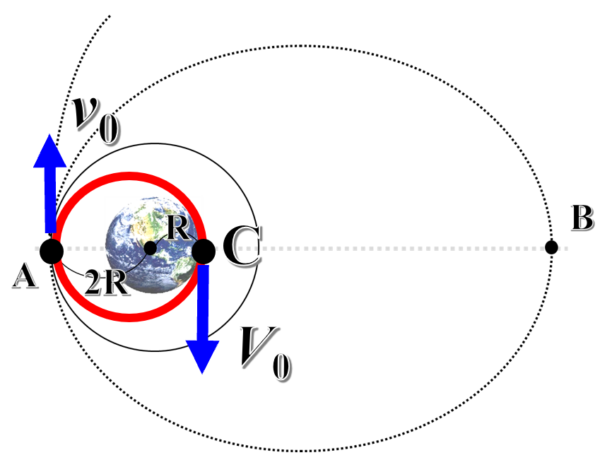

物体はだ円軌道を描いているので面積速度一定の法則とエネルギー保存則を使います。

この2式を連立して、v0を求めると次のようになります。


これより早ければ、地球に衝突することなく物体はだ円軌道します。
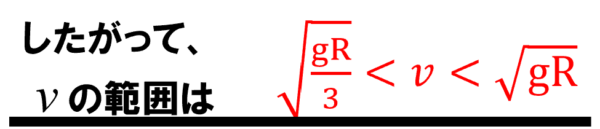
よって、これらをまとめると速さvの条件はこうなります。

どうでしたか??
最後の問題は、vの条件を考えるのが少し難しかったかもしれませんが、この問題を通して円軌道であれば運動方程式、円軌道以外の軌道であれば、エネルギー保存則、そしてだ円軌道であればケプラーの法則を利用すれば、自ずと解答が導かれていくことがわかっていただけたかと思います。
万有引力の問題は、一見したところ運動が複雑で解答が難しいイメージをもってしまいがちですが、物体の軌道によって解法が定まります。

このような理屈をきちんと押さえていけば、自分の領域、つまり高校の教科書の知識に持っていくことができます。
これで今回の解説は終了となりますが、皆さんも、一度問題に当たってみて、万有引力の問題解法を自分のものにしていってください。