
はじめに
それでは、次の主役はケプラーからニュートンに移ります。
万有引力の法則

万有引力の法則。「よろず」のものが「ゆうする」引力と書きます。
互いに質量がある物体は、引き合うという法則です。
例えば、ここ(左側)に質量Mの物体があります。

そして、ここ(右側)に質量mの物体があるとします。
中心から中心までの距離をrとします。

そうすると、互いに引き合う力が働く…
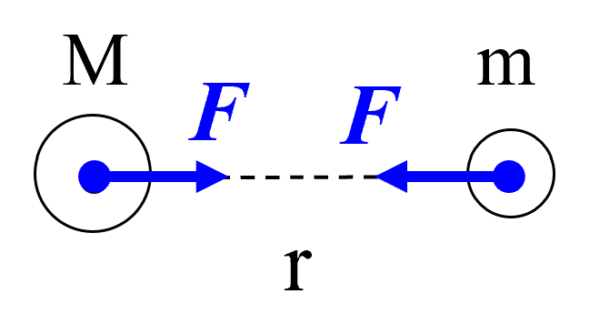
こういうわけです。
このときの力の大きさは、比例定数をラージGとして、
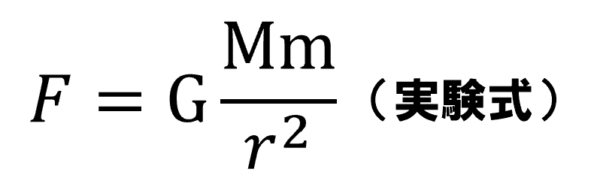

距離の2乗に反比例し、質量に比例した力が働く…、Gは、万有引力定数と呼ばれる比例定数です。
比例定数が入っているという事は、実験式ということになります。
この式は、実験から出てきたものですから覚えてください。

しかし、ここで1つ疑問が残ります。

万有引力の法則はニュートンが導いたと言われています。では、いったいどうやって実験したのでしょうか??
今、ここに私がいます。私の体重は70キロぐらいです。

たとえば、目の前に、体重が30キロくらいの子どもがいたとします。
そうすると、私には質量があります。その子どもにも質量があります。それなら引き合うはずですが、ぎゅ~っと引き合う(力を感じる)ことはないですよね。

それは、このラージGがすごく小さいからです。
だから、相手が地球みたいにすごく重たいものだと引っ張られて、それを我々は重力という訳で・・・

つまり私たちは、いつも地球に引っ張られているわけです。
だから皆さんは、こうやって床の上に立てるんです。それは、地球の中心に引っ張られているからです。
地球は、太陽の周りをグルグル回っています。

太陽に向かって落ち続けているわけです。それは、この力(万有引力)のせいです。そのせいで、グルグル回っていられるんです。

それはそれでいいのですが、それでは、いったい、どうやってこの力を測ったんでしょうか…??
1600年代です。

一体どうやって、そんな弱い力を測定できるんでしょうか…??
実験式と言いましたが、そんなに簡単に実験できるものではありません。
1700年代の後半から1800年代においては、もう一つクーロンの法則、つまり電荷と電荷が引き合う力、電荷と電荷が反発する力が確認されましたが、これは比較的楽です。

それは力が大きいからです。
ゴム風船を膨らましてティッシュで擦ってやれば、壁に張り付きます。静電気力は目に見えて大きい力です。

ところが私と子どもの間ではグァ~っと引き合う力は、そう簡単に観測されません。それは力が小さいからです。だから、簡単に実験で表すことが難しいわけです。

それでは、どうやってニュートンはこれを導いたのでしょうか…??
そこのところはちゃんとしておかないといけません。それではいきます。
万有引力の法則が導かれるまで
ラージMのまわりをスモールmの物体が円運動しているという風に考えます。

地球の周りを月が回っているということで結構です。その時に月は地球に向かって落ちなければなりません。
何らかの力が働いてなくてはならないということになります。
これは、円運動の時にも話しました。円運動なので、円の中心方向に加速度が存在しなければなりません。
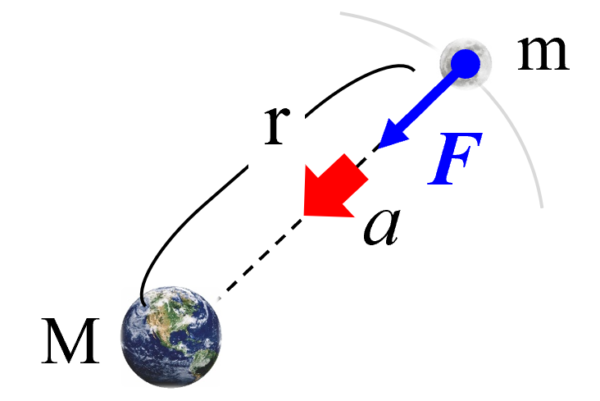
そこで、まず運動方程式を立ててみます。ニュートンは天上界においても、運動方程式が成り立つと言ったわけですから、運動方程式は…

質量mの物体に加速度aを生じさせたのはFである。
ただし、円運動です。

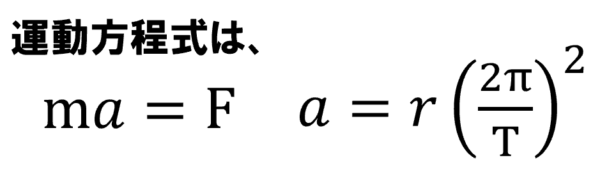
角速度に1周まわる時間をかけたら360度になるという関係を利用しています。これを利用した理由の説明は少し待ってください。
ニュートンは、地上界でも天上界でも同じ式が成り立たなければならないと言いました。だから、りんごが落ちる時と同じです。りんごが落ちる時は、ma=mgとなりますが、それと同様に式を立てたわけです。それに対して、加速度は特別な表記を持っている。そして、ここまで来たわけです。

ということは、さらにこの加速度のT2は、r3に比例しなければなりません。

そうすると、rが消えて、
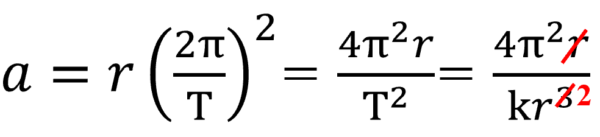
rの3乗が2乗になります。そうすると、加速度は、kr2分の4π2です。これを運動方程式に代入してみます。すると、こうなります。
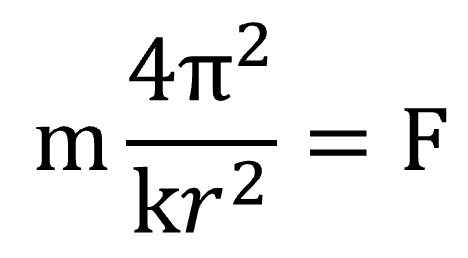
ここで4π2、πは3.1415…となりますから、これは定数です。そして、分母にあるkは定数です。この式から、何がわかるのかというと…
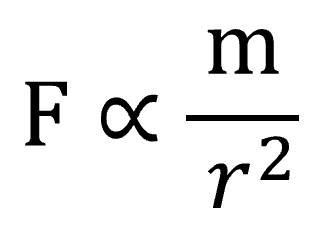
Fの右にあるのは、比例するという意味を表す記号です。

すごいですねぇ…
ケプラーの第3法則が正しいとするならば、月にはたらいている力というのは、rの2乗に反比例し、月の質量に比例するという訳です。

それでは、続けて行きます。
先ほど月にはたらく力について示しましたが、これを逆に月面上でみたらどうでしょうか。こうなってなければならないはずです。
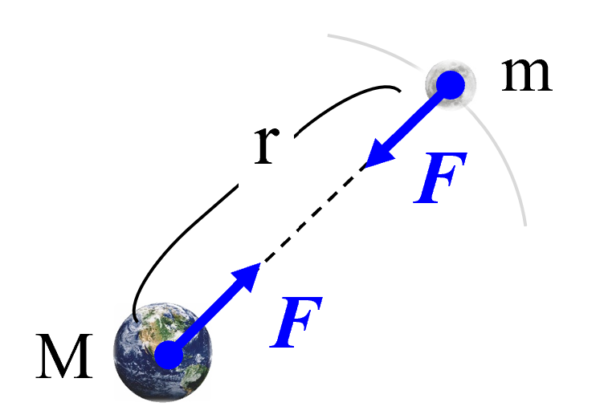
作用反作用の法則が働きますから・・・。ということは、次は、この月に乗っかって円の運動方程式を立てようとすると、質量mがMに変わるだけです。
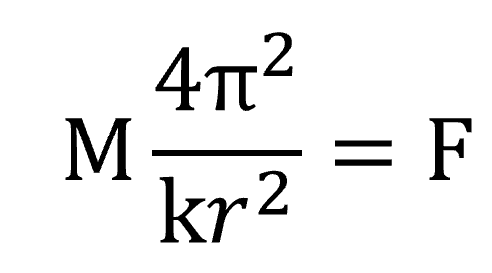
したがって他方から見ると、こうなるはずです…。
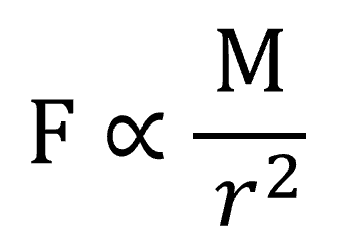

地球上から月を見れば月は回っているのと同じように、月面上から地球を見ると地球は回っています。
この2式を合わせて、比例定数をGとすると、こうなるわけです。
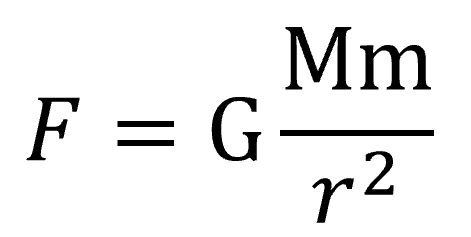
これは実験式ですから、どこまでrの2乗に対して、正確に反比例するのかっていうことが研究されています。少なくとも太陽系の惑星についてはrの2乗に反比例することは実証されています。

これは、さきほど実験式と言いましたが、今まで理論でずっと話を進めてきたから理論式ではないかと思われるかもしれません。
しかし違います。これは理論式ではありません。

途中でケプラーの第3法則入れています。ケプラーの法則は、観測データから出てきたものです。
ここに観測データを入れたという事になると、これは理論式とは言えません。したがって実験式です。
ですから、たとえばケプラーの法則で比例定数がkだとか4π2とか、そういうのがいっぱい出てきましたが、そういうものを全部ひっくるめてGにしているんです。だから、ここに比例定数があるんです。
比例するという事はわかっている。これが、発表された100年後にキャベンディッシュという人が、正確にこのGを求めるということに成功しています。

かなり大変な作業だったみたいです。ものすごく大きな鉄球をぶら下げて、どれくらいの力で引き合うかということを実際にやっています。
この実験のことは、皆さんが使っている教科書に載っていることがあります。
ニュートンは実際に測定したわけではなく、後ほどGが測定されるわけです。こうして万有引力というものが見つかってきて、例えば地球と月の間、例えば地球と太陽の間、そういったものは、この力によって運動しているということになります
高等学校の間では、地球を考える時は、地球と太陽がある。月を考える時には、地球と月の間だけを考えればいいことになっています。
要するに二体問題として考える事になるわけですが、ここに地球があって、月があって、太陽があって、そこで互いに万有引力が働き合って・・・ということをやり始めると、大変なんです。

だから、それは大学に行ってからやりましょう。
今は、二つの間でどれくらいの力がはたらくかを、まずは正確に理解することが大切です。

















