目次
はじめに
割合の後半パートでは、まず【参考】として、歩合と百分率について紹介しておきます。
□割合について1から学び直したい人は、こちらの記事を参考にしてください。
□動画による解説はこちら↓↓↓
歩合と百分率について
歩合と百分率も割合の1種であると考えてください。
ただし、割合と異なる点があります。

割合が、もとにする量を 「1」 とみたときの、比べられる量であるのに対して、歩合は、もとにする量を「10」、百分率は、もとにする量を「100」としています。
それぞれの関係を次の表にまとめていきます。

表をみると割合の値に比べて、歩合と百分率では、それぞれ10倍、100倍になっていることがわかります。

割合の計算を行うと、小数を含んだ数値になってしまうので、数字が読みづらかったりすることがあります。そのような時に、10倍、100倍することで、数値の大小関係を見やすくすることがあります。
そして、どれが割合で、どれが歩合や百分率かを、区別するため、
歩合には「割」(わり)、「分」(ぶ)、「厘」(りん)、
百分率には「%」(ぱーせんと)
という単位を後ろにつけます。

スーパーの食品売り場に行くと、2割引きとか20%引きというシールが貼ってあることがありますが定価の0.2だけ割引しますと言われてもパッと想像しにくいですね。
こういう時に、歩合とか百分率が利用されます。
百分率を使った計算例
それでは実際に、百分率を使った計算の例を確認してみます。
80gは400gの何%か?
「何%か?」という百分率を聞いているので、これは割合の問題です。

この問いが、「80gの食塩を溶かした食塩水400gの質量パーセント濃度はいくらか?」という表現に変わったら、濃度計算の問題になります。しかし、計算そのものは変化しません。
前回の記事では、中学、高校で学習する濃度計算に苦手意識をもつ中高生が多いという話をしました。
濃度計算というのは、液体の濃さを比べるための計算方法です。

その濃度計算の方法というのが、言ってしまえば「割合」なんです。
液体全体の質量を混ざっている物質の質量で割る。
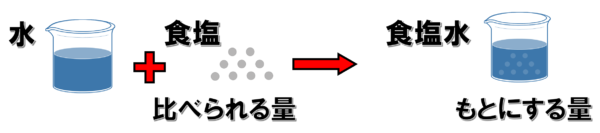
液体全体の質量が「もとにする量」で、混ざっている物質の質量が「比べられる量」です。

液体に混ぜた物質の質量だけでは、液体の濃さは比較できません。だから、混ざっている物質の質量を液体全体の質量で割った値で濃さを比較しようというのが濃度計算です。
それでは実際に求めていきますが、「もとにする量」は400gで「比べられる量」は80gです。
従って、割合は80÷400を計算して0.2という結果になります。
![]()
さて、これで割合が求められましたが、答えは百分率で答えないといけません。

先ほど説明した通り、割合では「もとにする量」を1、一方、百分率では、「もとにする量」を100として考えます。
したがって、求める答えは、0.2を100倍して20%ということになります。

それでは次の問題に行きます。
300gの15%は何gか?
割合の計算を参考にすれば、300g×15%が計算式となりますが、100で割るのを忘れないようにしてください。
従って、300gの15%は、45gとなります。


この解説が分かり難いという人は、次のように考えてください。
15%という割合は、もとにする量を100とした時に、「比べられる量は15である」という関係が成り立つということを意味します。
その関係が成り立つ時に、「もとにする量が300だったら、比べられる量がいくらになるか?」を考えます。
この時、比べられる量をxとすると、
15:100=x:300
という比の関係が成立します。
これよりxを求めると、45gという結果になります。

比とは…
ここで比の関係が出てきたので、比について確認しておきます。
「比」とは、2つの量や数値の大きさの関係を表すための言葉であり、比率や割合を表現するために使われます。

例えば、ある長さの物体Aが別の長さの物体Bの2倍である場合、AとBの比は「A:B=2:1」と表現されます。
同様に、ある物体Aの重さが別の物体Bの重さの3分の2である場合、その比は「A:B=2:3」と表現されます。

長さの例だと、もとにする量が1、比べられる量が2、割合は2。
重さの例だと、1をもとにした割合が3分の2なので、もとにする量が1、比べられる量が3分の2。
整数に直してやると、2:3というように、割合の関係を比を使って表現することがあります。

また、A:Bという比がある時に、A÷Bで求められる割合の事を比の値と言います。
先ほどの比の式だと、2:1であれば、比の値は2÷1を計算して2となり、2:3の比であれば、2÷3を計算して比の値は3分の2となります。
比の性質①
比の式には、比の値が等しくなる数字の組合せになっている比が同じになるという性質があります。

たとえば、2:3 と4:6の比ですが、

この2つの比の値は、3分2と6分の4。6分の4は約分すると3分2となるので、同じ比の値であることがわかります。
そのようなときは、2:3=4:6 と表現することが出来ます。
このように2つの比を等式で示したものを比例式と言います。

比の性質②:外項の積=内項の積


この性質(比の性質①)を利用すると、ある整数において A:B=C:Dであれば、AD=BCであることが証明できます。
A:B=C:Dの比例式が成り立つ時、A:BとC:Dの比の値も等しくなるので、
B分のAイコールD分のCという関係が成り立ちます。
この式の両辺にBDをかけて分母をとってやると、AD=BCという関係が成り立つことがわかります。


これを、外項の積と内項の積が等しいと言います。
この関係を利用して、比例式を解くことが出来ます。
比例式を解く問題
例えば、
x:35=2:7
であれば、
外と外、中と中とかけ算した式が等しくなるので、
7x=35×2 したがって、x=10
となります。
4:5=x:2 であれば、
5x=8 が成立して x=1.6 となります。
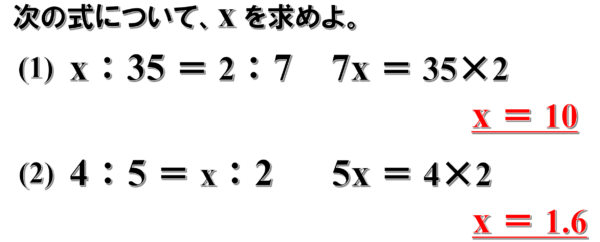
割合と比の違いについて

割合と比は本質的には同じことなのですが、1点だけ違うところがあります。
割合は2つのものを比較する時に用いられる量に対して、比は3つ以上のものを比較する時にも利用されます。
例えば、3つの角が 30°、60°、90°である直角三角形がABCとPQRがあったとします。
辺の長さが、△ABCでは斜辺が2、高さが1、底辺がルート3で、
△PQRは斜辺が8であることだけがわかっているとします。
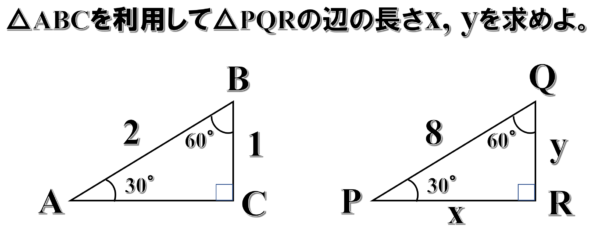
この時に、三角形PQRは三角形ABCを均等に拡大した三角形であることがわかるので、PR, QRの長さをそれぞれ x, yとすると、

という比が成立します。
斜辺の長さを比較すると、三角形ABCが2、三角形PQRが8であることがわかるので、△PQRは△ABCを4倍に拡大した三角形であることがわかります。
したがって、xとyは、三角形ABCの底辺と高さをそれぞれ4倍したものになるので、xとyは次のようになります。
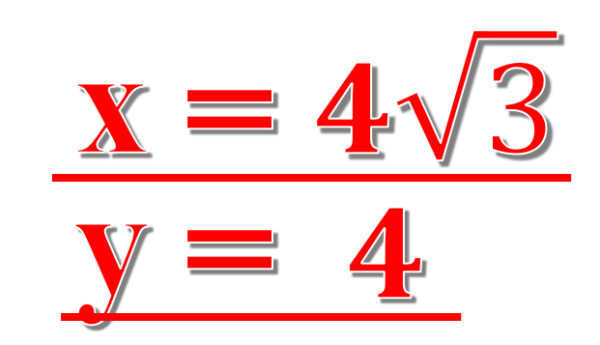
これで割合に関する説明は以上となります。

今回の動画を通して、小学校で学習する割合は、中学校、高校の内容とも密接に関わっているものであることが分かっていただけたかと思います。
もしも、化学の濃度計算であったり、物理の速さの関係がわからないという場合には、そこの単元を学習するだけではなくて、一度、
割合とは何だったか?
という本質的なところに戻って学習するようにしてみてください。