危険物資格取得のための高校化学No.20 物質量

それでは、今日の講義を始めよう。
この茶わんに1杯のご飯を盛る。この時、ご飯が１５０ｇあったとすると、茶わんの中に米粒は何個あるだろうか？

こんな質問をされた時、みんなはどうする？実際に米粒を1粒1粒数えてみるかい？骨の折れる作業だが、最後の1粒まで数えたら、きちんと答えは出る。

しかし、もう少し楽な方法がある。米粒の質量が全て同じであると考えて、米1粒の質量を図ってみる。すると０．０５ｇだった。であるとするならば、０．０５ｇの米粒が集まって、１５０ｇのご飯があると考えると、米粒の数をｘとすると、０．０５×ｘ＝１５０という式が成立する。

したがって、ｘは１５０÷０．０５で計算出来て、米粒の数は３０００個であると結論出来る。

これを踏まえて今日の本題だ。
ここに質量数１２の炭素原子が１２ｇあったとすると、炭素原子は何個存在するだろうか？？

先ほどの米粒３０００個であれば、たとえ面倒くさかったとしても、直接、お米を手にとって数えることは出来る。しかし、今回の炭素原子は、あまりにも小さすぎて、手にとることは出来ないし、仮に超高性能の顕微鏡で確認できたとしても、１つ２つとカウントしていたら、君たちの寿命がいくつあっても足りなくなってしまう。

ということで、炭素原子の１個の質量を図って、それが集まった結果１２ｇになったと考えていこう。
質量数１２の炭素原子の質量は、１.９９２６×１０－２３ｇだから、炭素原子の数をｘとすると、
１.９９２６×１０^－２３×ｘ＝１２　という式になって、ｘ＝６.０２×１０^２３となる。

このように計算すると、実際に存在する炭素原子の数を求めることが出来る。

ということで、今回のポイントを確認しよう。

この３つのポイントについて順番に説明していこう。

ポイント１：1モルの炭素原子の数を求めることは、茶わん1杯に盛られたご飯の米粒を求めることと同じである。

これは、さっき確認した通りだな。
ご飯を１回盛ると、１５０ｇだ。米粒１コは０．０５ｇだから、お米の数は３０００個。２回盛って2杯のご飯になれば、お米の数は2倍の６０００個だ。

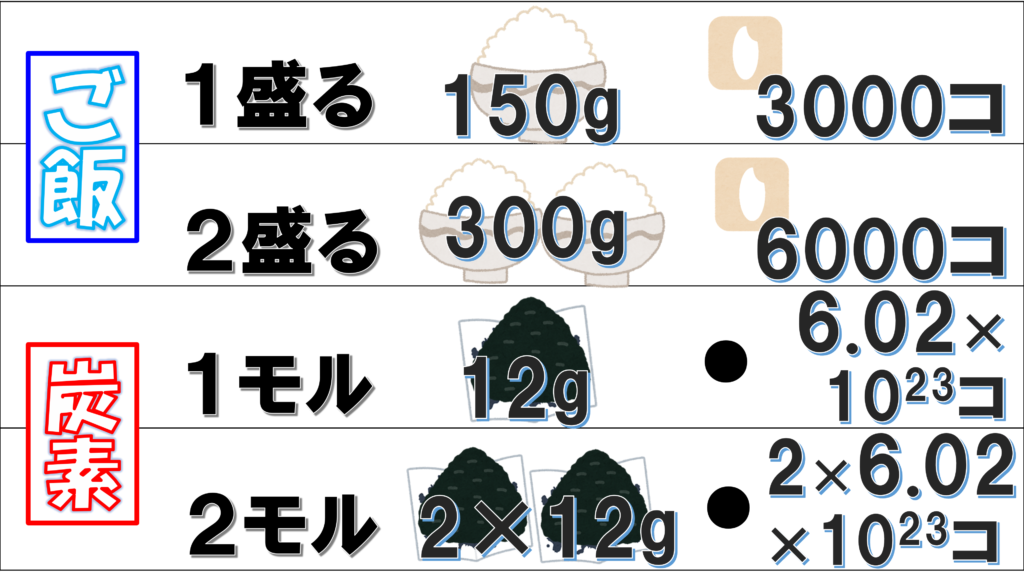
炭素原子は１回盛ると、１２ｇ。原子１個は１.９９２６×１０^－２３ｇで、原子の数は６.０２×１０^２３個。２回盛ると、６.０２×１０^２３×２個だ。

■ポイント２．1molの炭素原子について

今、確認したこの関係。大切だから整理しておこう。質量数１２の炭素１２ｇに存在する炭素原子６.０２×１０^２３個という数。この数は、とても大切だから名前が付けられていて、アボガドロ数という。
そして、６.０２×１０^２３個を１つのまとまりとした単位をmol（モル）といい、単位molを使って表した物質の量のことを物質量という。

ご飯の例に当てはめると、
茶わんに１杯盛ったご飯に存在する米粒３０００個がアボガドロ定数に相当する。

３０００個の米粒の物質量、もしくは茶わん１杯１５０gのご飯の物質量はいくらかと聞かれたら、１モルと答える。

２杯のご飯なら物質量は２モル。３杯のご飯だったら３モル。４杯なら４モルという。

この関係は、とても大切だからよ～く覚えてもらいたい。

■ポイント３．1molの質量について（モル質量）

さて、ここで確認した炭素原子１２ｇには、更に深い意味が隠されている。１２ｇの１２という数字は、炭素原子の質量数の１２であり、相対質量の１２のことでもある。

相対質量から、原子量を求めるということを前回学習したな。
炭素原子を相対質量の基準として、他の原子の相対質量や原子量については、炭素原子との割合を考えることによって決定するということだった。ということは、１モルの炭素原子が１２ｇであれば、原子量１の水素原子１モルは、１ｇ、原子量１６の酸素原子１モルであれば１６ｇと言うように、他の原子や分子１モルの質量は、原子量や分子量、式量にグラム単位をつけた値になる。

つまり、原子量や式量の値にｇ単位をつけたら、その物質が６.０２×１０^２３個　存在することになるのだ。大変便利ではないか？酸素原子は１個、２.６５６×１０－２３[g]だから、これに６.０２×１０^２３個を掛けると・・・

なんて、面倒くさい計算はやらなくていい。他の物質１モルの質量については、すでに知っている原子量や分子量、式量にグラム単位をつけたらいいだけだ。

この物質１mol あたりの質量のことをモル質量という。

整理すると、

単位ジースラッシュモルで表現して、これをグラム毎モルとかグラムパーモルと読む。

つまり、モル質量は物質の質量を物質量で割ることによって求まる１モルあたりの質量であるということだ。

それでは、今から例題を解いてみよう。

1molとは、6.02×10²³個のことなので、この消しゴムの数は、２×6.02×1023＝12.04×10²³個となる。1.204×10²⁴個としても正解だ。

1molとは、6.02×10²³個のことだから、6.02×10²³分の3.01 × 10²³で約分をすると２分の１となり、小数だと０.５molになる。

それでは、最後の問題だ。

水酸化ナトリウムNaOHの式量は、　23 + 16 + 1 = 40 なので、水酸化ナトリウムのモル質量は、４０[g/mol]となる。

さて、今日の講義はここまでとしておこう。それでは、次回の授業でまた会おう。

今回の学習は、ここまでです。

◎異なる単元の学習は、こちらのガイドを活用ください。