危険物資格取得のための高校化学No.19 原子量・分子量・式量

今回は、原子量について説明しよう。
今から話すポイントは、

以上の３つだ。

１．同位体を含めた原子の相対質量の平均値が原子量である。

前回の授業で、相対質量について学習したなぁ。

原子の質量は、数字で表現すると細かくて扱いにくい。だから、炭素原子の相対質量を１２として、これを基準にする。その他の原子の相対質量は、割合を求めることで決定していこう。という話だったな。

そうすると、全ての原子の相対質量は、質量数と大体同じ値になった。

ところで、炭素原子には、質量数が１２のものの他に質量数が１３や１４のものがある。これらを互いに同位体と言ったわけだが、実は、自然界に存在する炭素原子の中には、異なる質量数の原子が一定の割合で存在することがわかっている。

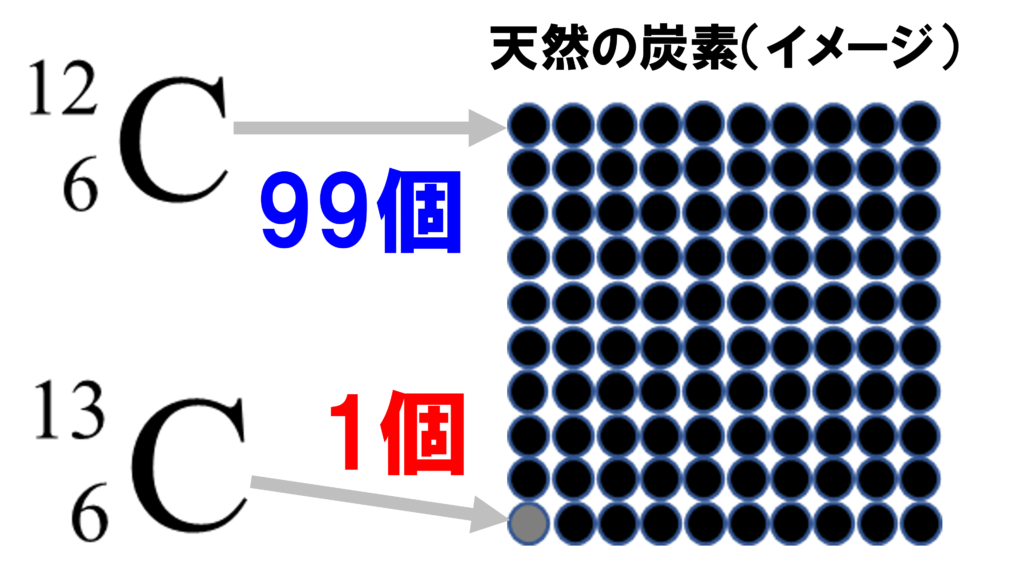
例えば、100個の炭素原子があったとして、99個の炭素原子の質量数は１２、残りの1個の炭素原子の質量数は１３だったとした時に、炭素原子の平均の相対質量はいくらかと聞かれたら、明らかに１２より少し大きな値になっていることがわかるだろう。

実際に、自然界に存在する炭素原子を相対質量で表現する時には、質量数の異なる炭素原子を含めた平均値を考えないといけない。

このように、同位体を含めた原子の相対質量の平均値のことを原子量という。

２．平均の質量は、質量の合計を、合計した数で割ることで求められる。

今から、この原子量を実際に求めていくが、その前に平均値の計算方法を確認しておこう。

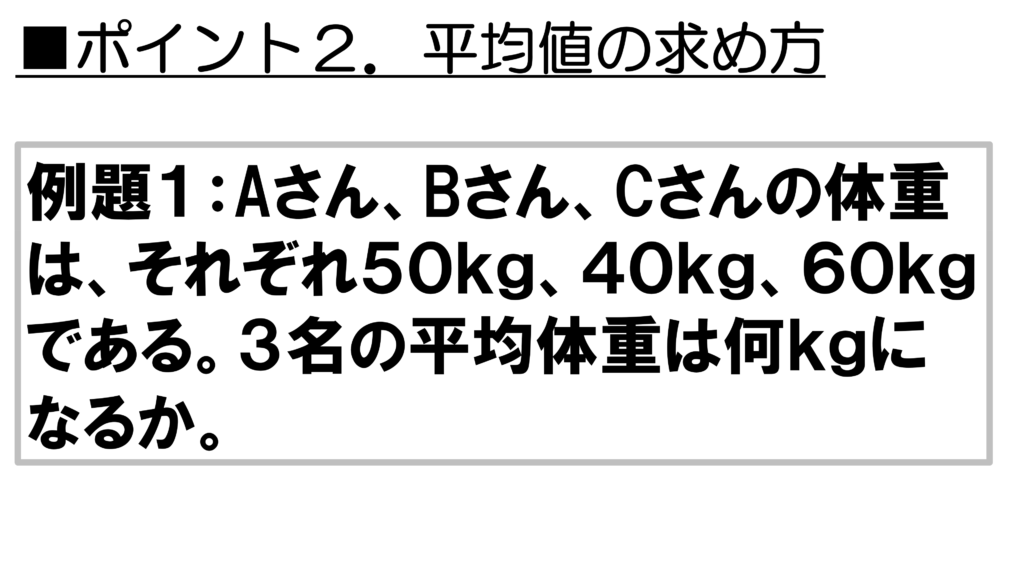
平均値を求めるためには、まず与えられたデータを全て足して、その結果をデータの数で割るとよい。例えば、今回の問題だと、全てのデータを足すと、５０＋４０＋６０で１５０となる。
データの数は3個だから、１５０を３で割ると、求める平均体重は５０ｋｇとなる。

原子量を求める計算についてもこれと同じだ。数字が少し複雑にはなるが、パニックにならないようについてきてもらいたい。

９８．９３％と、与えられた数値に小数とパーセントという単位が含まれているので、単純に考えられるように、炭素原子が１００００個あると考えて、１００００個の炭素原子の平均値を求める問題に置き換えよう。

炭素原子が１００００個あるとしたら、¹²Cは９８.９３％ある訳だから、炭素原子が１００００個あるとしたら、９８９３個、¹³Cは１.０７％だから１０７個になる。

原子量を求めるということは、相対質量の平均値を求めることだから、平均値の計算方法に従って、炭素原子１００００個の相対質量を合計してみよう。すると次のような式になる。

これをデータの個数、つまり１００００で割れば、平均値が求まるから、
１２０１０７÷１００００で答えは１２.０１０７となる。

３．原子量を用いて、分子やイオンの質量を表したものを分子量、式量という。

最後に分子量と式量について確認しておこう。

今、水素Hの原子量を１、酸素Oの原子量を１６だとしよう。
それでは、水H₂Oはいくつになるか？
難しく考える必要はない。H₂Oは、H原子が２つ、O原子が２つあるから、この数の分だけ原子量を足せばいい。

つまり、1＋１＋１６＝１８となる。
このように水分子ついて原子量を足した量のことを分子量という。

つまり、分子量とは、分子を構成する原子の原子量の総和のことだ。

同じように、イオン式や組成式に含まれる原子の原子量の総和のことを式量という。

例えば、水素Hの原子量を１、窒素Nの原子量を１４とする時、
アンモニウムイオンNH4+の式量は、１４＋１×４＝１８

ナトリウムNaの原子量を23、塩素Clの原子量を35.5とする時は、
塩化ナトリウムNaClの式量は、 23 ＋ 35.5 ＝ 58.5　となる。