
はじめに
それでは前回の力のモーメントの講義に引き続き、問題の解説に入っていきます。
力のモーメントの問題
図のように、長さl、質量mの一様な棒を糸にとりつけ、棒を粗い壁に接するようにして水平になるように静止させる。糸と棒のなす角をq、重力加速度の大きさをgとして、以下の問いに答えよ。
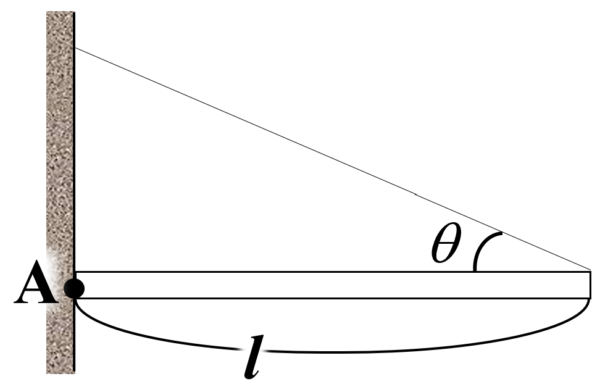
(1)糸の張力の大きさをTとして、点Aのまわりの張力Tのモーメントを求めよ。
(2)点Aまわりの重力のモーメントを求めよ。
(3)Tをmとgを用いて表せ。
(4)棒が壁から受ける垂直抗力の大きさを求めよ。
(5)棒が壁から受ける摩擦力の大きさを求めよ。
まずは、質量mの一様な棒とあります。
棒の質量はmなので、棒の重心の位置から重力mgが働きます。
この時、棒の端から端まで均質な重さで出来ていたら、棒の中心部分が重心になります。
しかし、例えば野球のバットのように端と端で太さが違っていたり、もしくは別の材質の物質で出来ていたら、棒の重さは均質ではないので、重心の位置が棒の中心からずれてしまいます。

こういう面倒くさいことを考えなくてもいいように、問題に与えられた棒は、均質の素材であるとして、棒の重心、つまり「重力の作用点は棒の中心にある」ものと考えられるように設定されています。

したがって、一様な棒と書かれていたら、重力は棒の中心から作用するものと読みとってください。

つぎに「粗い壁」という言葉は、「壁から生じる摩擦力を考えなさい。」ということを暗に意味しています。

逆に、摩擦力を考えなくてもよい場合は、「なめらかな壁」と表現します。
この問題の場合、棒にはたらく重力mgを支えているのは、棒の右側にとりつけられた糸からはたらく張力がその一つになります。
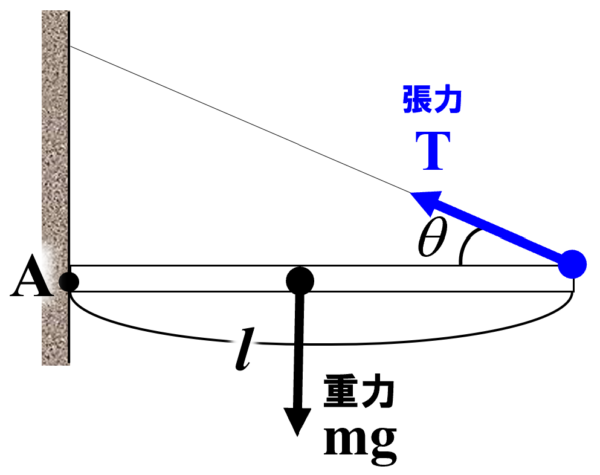
もしも、壁がなめらかな簡単につるつる滑りやすい壁だったら、この棒は左側からストンと下に落ちてしまいます。しかし、今回の問題では、ざらざらな粗い壁の摩擦力のお陰で、棒が図のように静止しているわけです。

それでは、実際に問題を解いていきます。
(1)解説
(1)糸の張力の大きさをTとして、点Aまわりの張力Tのモーメントを求めよ。
まずは、糸の張力から考えていきます。棒にとりつけられた糸には張力が働きますが、張力がはたらく方向は糸が伸びる方向になります。したがって、棒の右端から糸の方向に、張力を書き込みます。張力の大きさはTです。

さて、ここから張力Tのモーメントを求めるためには、うでの長さを求めないといけないので、点Aから糸の線に沿って、垂線を下ろします。そうすると、この垂線の長さを求めるわけですが、垂線の長さはlsinqとなります。
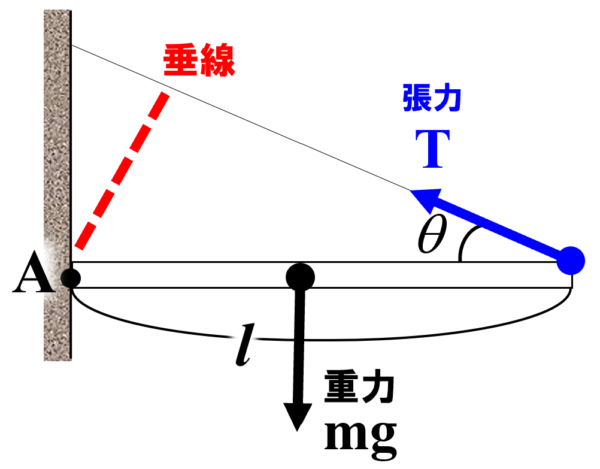
また、張力Tのモーメントの向きですが、これはAを回転軸とすれば、反時計回りに回転するように作用するので、モーメントは正の値をとります。
したがって、張力Tのモーメントは、Tlsinq となります。

それでは次に行きます。
(2)点Aまわりの重力のモーメントを求めよ。
次は重力のモーメントを考える問題です。先ほど説明した通り、一様な棒で出来ているので、重力が作用する位置は、棒の中心部分です。したがって腕の長さは、1/2 lとなります。
そして、モーメントの向きは、点Aを回転軸とすれば、時計回りに回転するように作用するので、モーメントは負の値をとります。
したがって、点Aまわりの重力のモーメントは、-1/2mglとなります。

(3)解説
(3)Tをmとgを用いて表せ。
今、この棒は静止しています。

ということは、この棒にはたらく回転力は互いに打ち消し合っていることになります。
これを数式で表すと、
Tlsinq=1/2mgl となります。

皆さんのわかりやすい方を利用してください。
これより、lを消去すると、T=mg/2sinq となります。
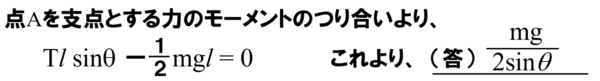
(4)解説
(4)棒が壁から受ける垂直抗力の大きさを求めよ。
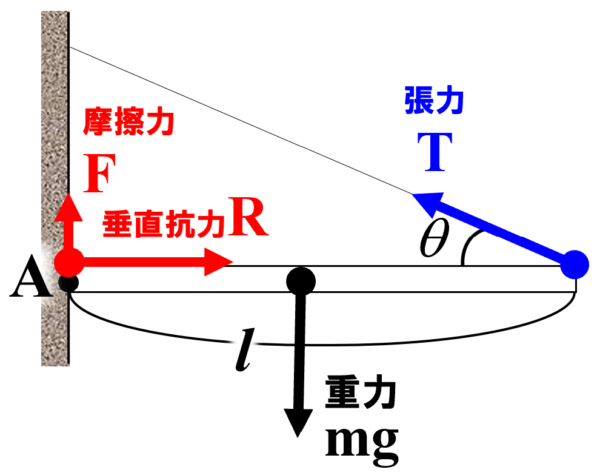
棒と壁は接触しているので、壁の面と垂直な方向に垂直抗力がはたらきます。
この垂直抗力をRとして図に書き込むと、このようになります。

棒は静止しているわけですから、この時、棒にはたらく力はつり合ってなければなりません。
したがって、ここでは、棒にはたらく垂直抗力Rと糸の張力の水平成分がつり合っていると考えます。

張力の水平成分は、Tcosqとなるので、
R=Tcosq (3)よりTをmとgで表すと、
R=mgcosq/2sinq
sinqとcosqをtanqに置き換えると、最終的にR=mg/2tanq となります。
それでは、最後の問題です。
(5)解説
(5)棒が壁から受ける摩擦力の大きさを求めよ。
まず、棒にはたらく摩擦力をFとして図に書き込みます。
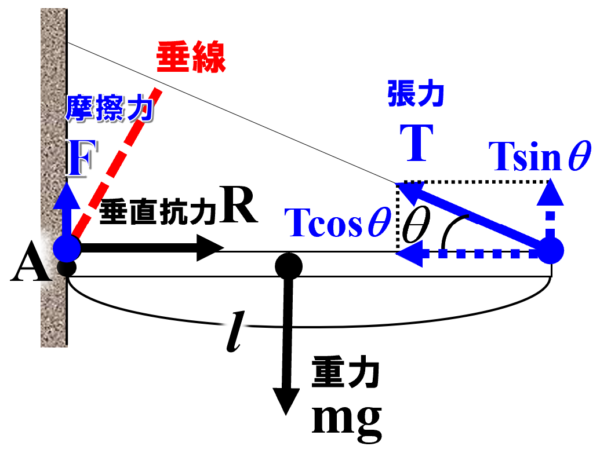
棒には重力mgがはたらいていますが、この下向きの力mgと糸の鉛直方向の成分、そして、壁からはたらく摩擦力がつり合っています。
糸の張力の鉛直方向の成分はTsinqとなるので、鉛直方向のつり合いを数式で表現すると、
mg = F + Tsinq
となります。
ここでTをmとgに置き換えてFを求めると、
F=mg-1/2mg=1/2mgとなります。















