目次
はじめに

前回講義の中で、覚えるべき式、定義をちゃんと理解した上で導出できる式を頭の中で区別できるようになれたでしょうか…?
□前回の復習
とは言っても、一度講義を聞いただけでは思うように頭の中には入ってこないと思いますから、こういった時には練習問題が大切になってきます。
ここでも、ただ式を丸覚えして、その中に値を代入して、

よし正解した!
自分はわかってるぞ!
という解き方をしていると、電気の問題の本質的なところがわからなくなってしまいます。

だから、問題を解く時にも、解き方に拘る必要があります。
電場とは何か?
電位とは何か?

皆さんにつきましては、1週間ほど時間が経ってから
もう一度自力で解いてみてください。
今回は、以前重要問題集に掲載されていたの「電場と電位」の問題です。
電場と電位の問題

(1)解説
(1)x軸上の点P(x,0)の電場のx成分とy成分を、それぞれ座標xの関数として求めよ。ただし、x>0とする。
電場を求める問題です。

点Pでの電場を求めよ!
という訳ですから、点Pに+1クーロンの電荷を置いてやるわけです。


これは見たらわかる通り、y成分方向に力は働いていないので、点Pの電場のx成分をEx、y成分をEyとすると、y成分の電場、つまり+1クーロンの電荷にはたらく力は0です。


そして、次にx成分です。
点Aから受ける力、ここでは+1クーロンあたりなので電場のことですが、これをEA、原点からの電場をE0としておきます。


片方の電荷が+1クーロンなわけですから、EAについては、Qのところに4qを代入します。距離はx+a が入ります。

E0については、Qにqを代入します。距離はx。
![]()


ここで注意しておかないといけないのは、これとこれを(EAとE0)足し算してはいけないということです。

そして、クーロンの法則から求めたクーロン力は力の大きさだけしかわかりませんから、力の向きを確認するためには、作図が必要になってきます。
作図の結果、x軸を正の向きとすると、電場のx成分は、ーEA+E0になったということで、この辺りの符号を含めた計算に注意してください。
(2)解説
次は電位の問題です。

座標xの関数として求めよと小難しく書かれてますが、電荷は全てx軸上にあるので座標yについては考えても仕方ないでしょうねぇ。
電位とは、+1クーロンあたりの位置エネルギーのことですから、まず、クーロンの法則による位置エネルギーを確認します。


このようになります。

ここでは、電荷は符号を含めて代入していることに注意してください。

位置エネルギーですからスカラー量です。
したがって、ここは足し算です。

電場はベクトル量、電位はスカラー量。
この辺の違いに注意してください。
エネルギーを足すということに違和感を覚える方がいるかもしれませんが、すでにこの計算には慣れてますよね。

エネルギーというのは能力のことだと力学分野で学習しました。
力学の重力による位置エネルギーは、高いところ落ちたり、斜面から滑り落ちる落下能力。それから動いている物体が持つ能力を運動エネルギー。

位置エネルギーと運動エネルギーを足したものが力学的エネルギーだ!
って計算してきたじゃないですか。

あそこでもエネルギーを足し算してましたよ。
ここでも同じことをやっているんです。
力学と違うところは、電荷のプラスとマイナスを含めて考えないといけないところで、そこのところが少し複雑になっていますが、きちんと定義を押さえながら進めていけば問題ないと思います。
(3)解説 および 電気力線・等電位線について
これは(2)と同じですよね。xy平面上の電位を考えないといけないから、xy平面に+1クーロンの電荷を置いてやったら問題が解けるわけですが、

ここで少し電気力線と等電位線について、必要なことだけ整理しておきます。
電気力線と等電位線

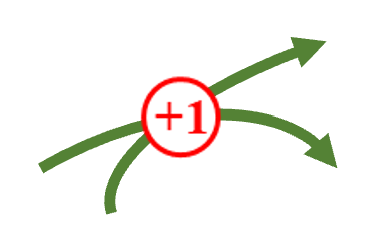
+1[C]の点電荷が移動する道筋のことです。
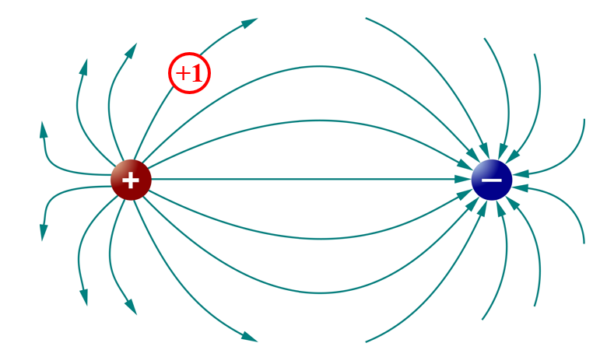
+1[C]である必要はありませんが、厳密な定義を持ち出してしますと、逆に難しくなってしまうので、ここでは考えやすいようにまとめて行きます。
プラス1クーロンの電荷を置いたら、どちら向きに力を受けるか!?

あの矢印が電気力線だというわけです。
教科書では平面的に書かれますが、現実の3次元空間だと栗のイガイガとかウニみたいになっているのでしょうか…??


電位が等しい点を線で結んだものです。
だから、地理学の等高線に相当します。


点Aには谷があって、原点に山があるわけです。
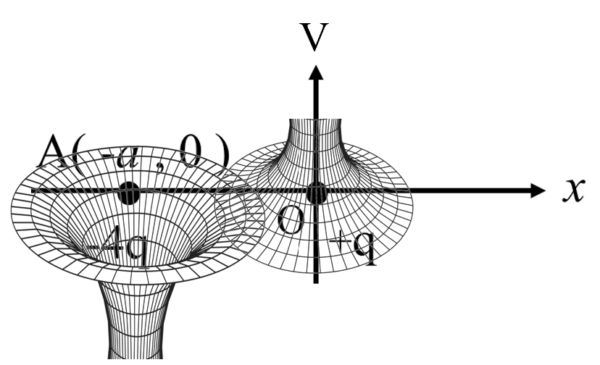
そして、点Aは-4qクーロンで電荷の大きさはqクーロンの4倍なので、谷の方が急斜面になっているんですね。

だから、-4qクーロンの近くに+1クーロンの電荷を置いたら、谷底に吸い込まれるように落ちていくでしょうし、
+qクーロンの近くに+1クーロンの電荷を置いたら、斜面をすべるように転がっていくでしょうねぇ。
そういうのを真上から見たのが等電位線です。

この図だと、このあたりの等電位線の図形を求めないといけないんですねぇ…。
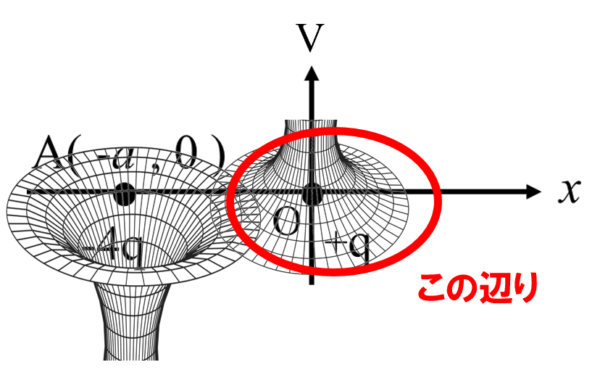
ここで等電位線がイメージ出来ていたら、その図形が円に近い2次曲線になってくることは推測できます。

それでは電気力線と等電位線の説明はこれくらいにして、(3)の問題に移っていきます。
(3)解説

電位が0になる条件を考えて、導かれた数式がどんな図形になるか?
を説明しないといけないわけです。
だから、まずはxy平面上の電位が0になる点について考えてみましょう。
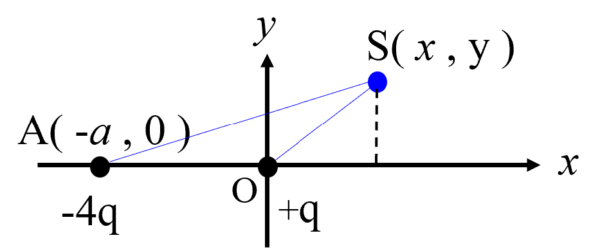
点A
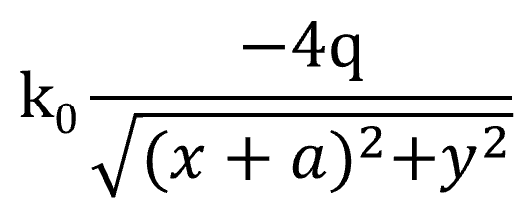
原点
![]()
Vsはこのようになります。
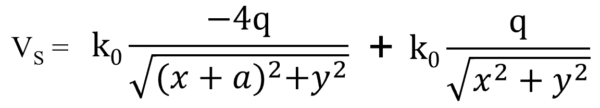

ここからは数学的に処理していくだけですね。
Vsが0になる時を考えるとこの式は、
となって、

x2とy2の関数になってますから、やはり2次曲線の可能性が高いですね。
それを踏まえて数式を変形してみると、こうなります。
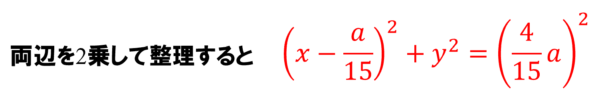

ちゃんと円になりましたねぇ…。
問題の続きは次回の記事で解説いたします。