はじめに

今度は、単振動の周期についてやっていきます。
周期ですから行って帰ってくるまでの時間です。この行って帰ってくるまでの時間をこれから求めていきます。
単振動の周期
単振動の周期を導出する

もちろんフックはこんな事はやっていません。しかし、ニュートンはここまで考えていました。
いや、むしろ考える程のことでも無かったのかも知れません。

なぜなら単振動の大元は円運動です。グルッと回っているだけです。その影が単振動です。ですから当然単振動の周期は、グルッと1周まわる時間と同じです。
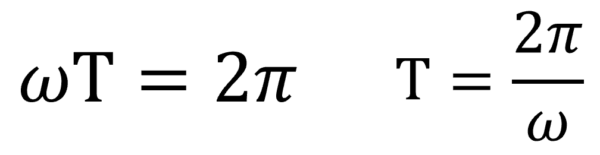

ωはどうやって求めればよいのか…?
加速度は、 a=ーω2xです。

これは、どこから出てきたのか?
それは、ここです。
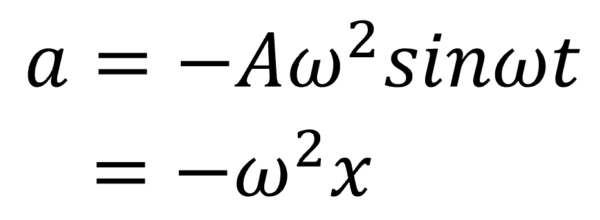
では、その下の運動方程式を見てみます。
![]()

すると、mω2はkに等しい… 。
mとωが定数なのでkに置き換えました。
フックが弾性力はxに比例する力であると言って比例定数をkとしたわけです。初めてこのkが出てきた時には、これはばね定数であると教わりましたが、理論的に分析してみるとmω2乗に等しいというわけです。

それでは、このkを使って周期を考えてみます。
ここでmω2=kより、wはいくらになるのかというと、
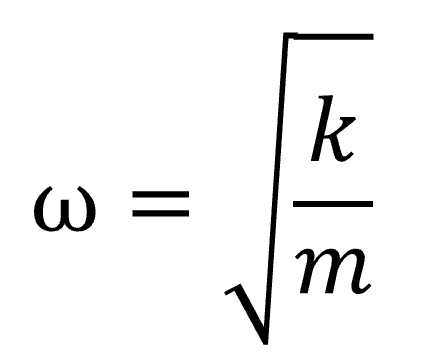
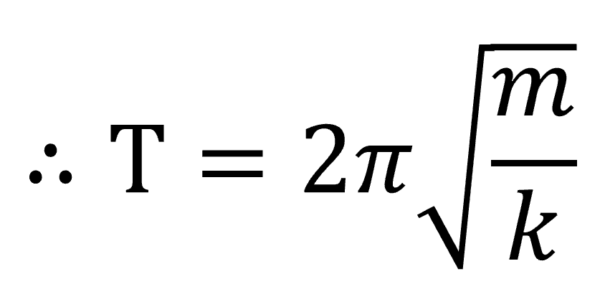

単振動を学習済みの方は、すでにこの式を覚えているかも知れませんが、どの様にして、この式が出来てきたのかは知っておいてください。
その時に、この2πを見落とさないようにしてください。

2πは360°という意味です。
これは元々円運動の式から来ているんです。

等速円運動の影が単振動なので、グルッとまわる時間と同じです。
本来、行って帰ってくるだけなので単振動には360°という概念はないはずです。それなのに2πが入っているということ。

円運動から来ていることが明らかなんです。
ところがこうしたことを一切考えずに、

Tイコール2πルートk分のmだ!
公式だぁ!
と言って、覚えるだけだと、それは後々物理の学習が辛くなってきます。覚えるだけの勉強だと楽しくはなれないでしょう。

何をするにしても、楽しくないと得意にはなれません。
物理においても例外ではなくて、昔の人たちがどうやって考えてきたのか、そう言ったことも含めて考えていく。

そうすると、分からないことが分かるようになるわけですから、それは面白いですし楽しいでしょう。
そういうところが分かってくると、入試問題の解法としても使えるようになってくるので、周期の式については、成り立ちも含めて頭の中に入れてください。
単振動の運動方程式について

さて、これで単振動の基本事項については全て確認しましたが、最後にもう少し単振動の運動方程式について考えていきます。
ここまでに考えてきた単振動は、最もシンプルであるというか理想的な状態について考えていました。例えば、今の場合だと滑らかな床の上にあるバネを「びよ〜ん、びよ〜ん」とさせてるわけですが、実際は、いつもそれだけというわけにはいきません。

まずは、滑らかな床の上にあるバネから考えていきます。
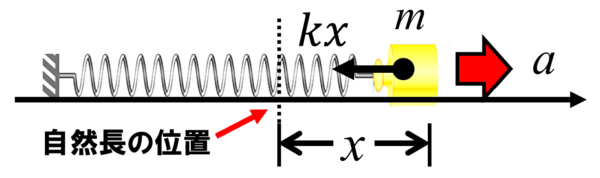
図の自然長の位置からばねがx伸びているとします。
右向きを正とします。

それでは運動方程式を立ててみます。
まず物体にはたらく力は、自然長の位置に戻ろうとする力が働くので左向きにkx
質量mの物体に加速度を生じさせたのは、逆向きの力kxである。
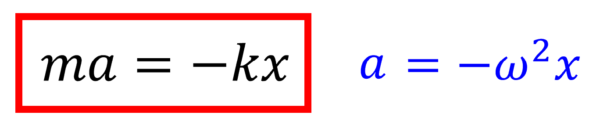
これでOKです。

それでは次に行きます。
今度は、鉛直下向きにばねがぶら下がっているとします。ばねは、自然長からx伸びているとします。
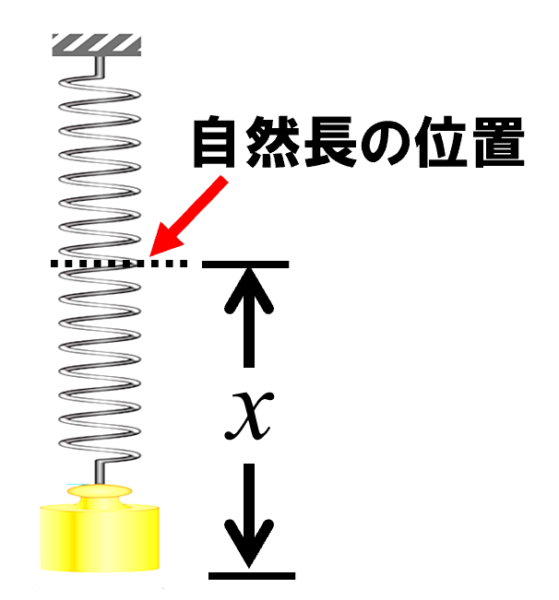
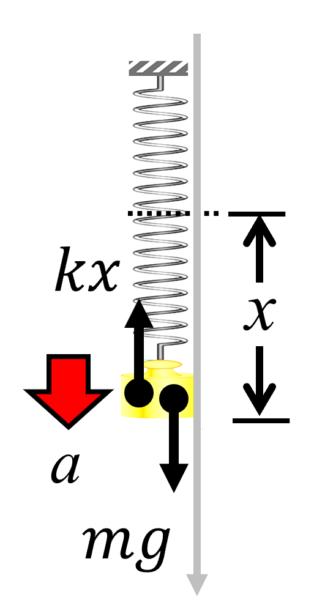

この式では、加速度がxに比例した物理量になっていることが確認できます。

この時に、加速度aはーω2xとして良いのでしょうか??

それでは、このばねは単振動しないのかと言えば、そんなことはありません。皆さんは、いずれのばねも単振動することを現象としては理解しているはずです。

しかし、こちらの場合は運動方程式を立てた時に、どうも式の解釈がうまくいかない。
単振動をするためには、加速度aはーω2x(に相当する)の表記を持っていないといけません。

そこで、この式ではこう考えます。
まずーkで括ります。
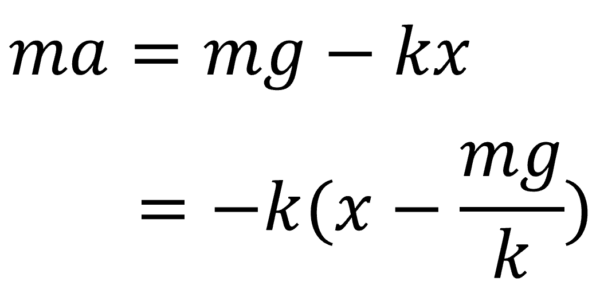

それから、括弧の中を見ると、xからk分のmg引いたと書いてあります。

これはxから一定の値を引いただけです。
従って、これをXに置き直します。
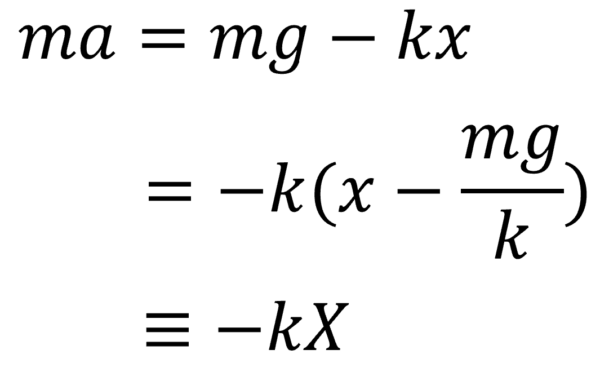

xとX。
xと言うのは基準からの「ずれ」を表しているわけです。

k分のmg…だけずれている…、


つまり、この単振動は自然長が振動中心ではなく、力のつり合うところが振動中心です。xがk分のmgになる時が0です。

滑らかな床の上ではxが0になる時が0、つまり振動の中心は自然長です。
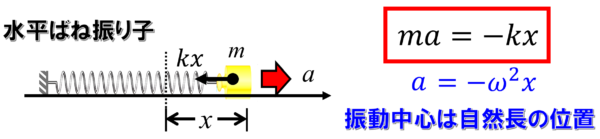
水平ばね振り子は自然長を中心として単振動しますが、鉛直ばね振り子はk分のmgだけずれたところが振動中心となって単振動しています。
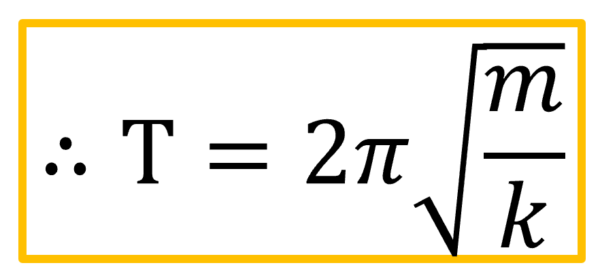

だから、周期の式は公式として覚えてしまっても構いません。
単振動の周期には重力加速度が関与しないので、水平方向で振動させようが、鉛直方向に振動させようが、宇宙空間で振動させようが関係ありません。