
はじめに
今回から力学的エネルギーと仕事について学習します。力学的エネルギーについては次回の授業で取り扱う事として、

仕事とエネルギーについては、一度物理を学習した人であっても、「この両者は、よく似たものである…」という浅い認識に留まってしまうところです。
しかし、物理という学問は、世の中で起きていることをなるべく簡単に理由付けして説明していくというスタンスです。

似たようなものであったら、わざわざ2つの用語に分類することはありません。
そこで、
仕事やエネルギーという言葉はどのような意味で用いられていて、数式で表すとどうなるのか?
というようなことを考えていきます。
1.仕事の定義
それでは、まずは仕事について見ていきます。
仕事とは、何らかの働きをして、一定の成果を残すために労力を注ぐことを意味する言葉として日常生活で利用されていて、様々な仕事が存在します。

物理では物体に対して力を加えて移動させたときに、物体にどれくらいの力を与えて、どれくらいの距離を移動させたかという「労力」を仕事として評価します。
そこで、高校物理では、仕事を次のように定義します。
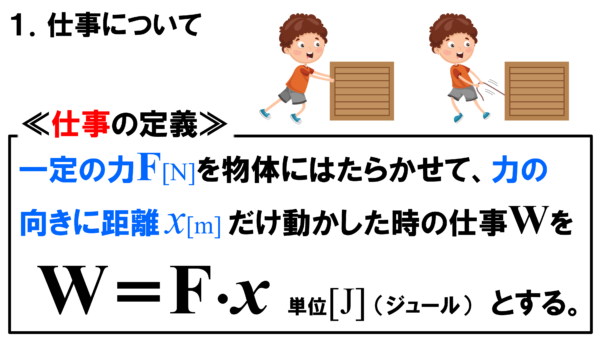
一定の力F を物体にはたらかせて、力の向きに距離 x だけ動かした時の仕事 W を W=Fx
とする。

こうして、我々が物体にWの仕事をしたとか、物体がWの仕事をされたと表現します。
仕事の単位は[J]と表現します。
物体に加える力が大きければ大きいほど、物体を移動させる距離が長ければ長いほど、その時の労力は大きくなります。
ほんの少しの距離しか移動させていないけど、大きな物体を移動させるためには、とても大きな力を必要としたから、

結構大変な仕事だったねぇ…
とか、

結構遠くまで運んだんだけど、対して力を使っていないからそれ程しんどくなかったよ…
という様に、合理的に労力を評価できるので、仕事の定義のことを力の距離的効果と言ったりもします。

物体に加えた力に距離をかけることによって、我々がした仕事を評価しようという訳です。
このようにして仕事というものが定義されます。
それでは、具体的な例を挙げて物体にした仕事をいくつか表現してみます。
床の上に物体があります。その物体に力Fを加えました。
その時に、物体がxだけ移動したら、その時の仕事Wは、Fxとなります。

もしも、仮に、物体に力Fを加えたとしても、物体がとても重くて、全く動かなかった場合、このときの仕事は、W=F・0で0と表現します。

たとえ大きな力を加えても物体を移動させられなければ、その成果は0。このときの労力は評価されないということです。
そして、次は、物体に糸をつけて引っ張ったとします。
地面に対して、q の角度で、斜め方向に力Fで引っ張り、xだけ移動させた。この時の仕事について考えてみます。ここでは、力Fの地面に平行な成分を考えます。したがって、物体にした仕事はW=Fxcosq となります。

この時、力の地面に垂直な成分はFsinq は、進行方向に対して垂直な力であり、x移動させるという仕事には貢献していません。

進行方向に対して垂直な力は、仕事として評価されません。
したがって、物体の移動方向に対して垂直な力がした仕事は0になります。

仕事の定義を、「移動方向に対して作用した力を考える」と定めたわけですから、物体の移動に関与しない力による仕事は評価しないわけです。
定義をきちんと押さえながら確認していくと、よりよく理解で出来るようになります。

それでは、次に行きます。
物体をxだけ移動させたときに、床から摩擦力がはたらいていたとします。
このとき、摩擦力がした仕事は、W=-Fxと書けます。進行方向に対して、逆向きにはたらく力なのでマイナスということです。


進行方向に対して、逆向きに力が作用するということは、x進むという仕事の邪魔をした。
邪魔をしたということに関しては、負の仕事をした!
という方が、より現象に即したと解釈になります。こうしてプラスの仕事とマイナスの仕事を考えていきます。
仕事についての説明は以上となります。
続いて、エネルギーに移っていきます。
運動エネルギーについて
エネルギーという言葉。

これは仕事をする能力とまず捉えてください。
あの人は能力があるから、これだけの仕事を任せることが出来る!
とか、

あれだけの仕事を1人で出来るという事は、
とても能力があったんだなぁ…
という言い方を日常生活でもすると思います。
そのようなイメージを持ちながら、物理における仕事とエネルギーの関係を確認していきます。

まずは、運動エネルギーについてからです。
運動エネルギーとは、運動能力と言い換えることが出来ます。
これから物理における物体の運動能力を考えるために、等加速度運動を例として考えてみます。
右向きを正として、ある所に物体が静止していたとします。

この物体が、何らかの力(一定の力)を受けたことによって、xの位置に到達するとします。
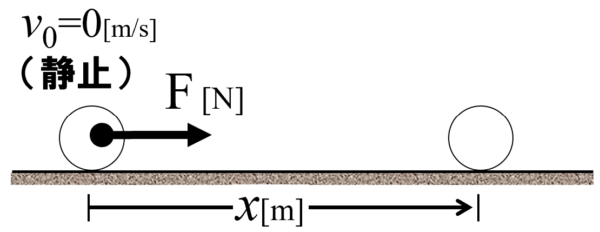
この時、v という速度を持ったとします。
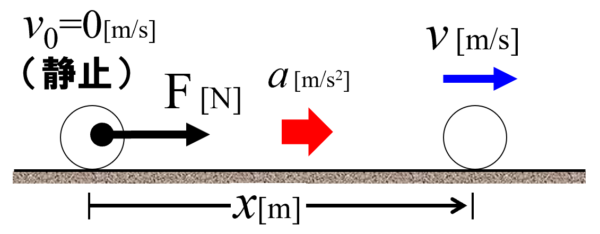

最初は運動能力を持っていませんでしたが、xの位置では運動能力を持っています。このような設定でこれから考えていきます。
この時、速度が変化しているので、物体に生じた加速度をaとします。
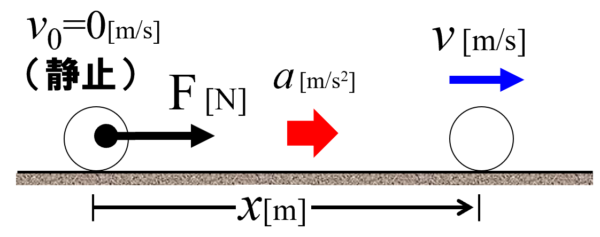
ここで、図を参考にしながら等加速度運動の3番目の式を使うと、次のような式が成立します。

この図において、最初止まっていた物体が動き出しました。

ということは、この時、何らかの力がはたらいたはずです。
その力がFです。
今、等加速度運動しているという前提で話しています(力Fは一定なので)。

ですから、加速度は一定です。
加速度が一定であるということは、運動方程式を考えると、ma=Fですから、(図にある)このaに質量mをかけると力になります。
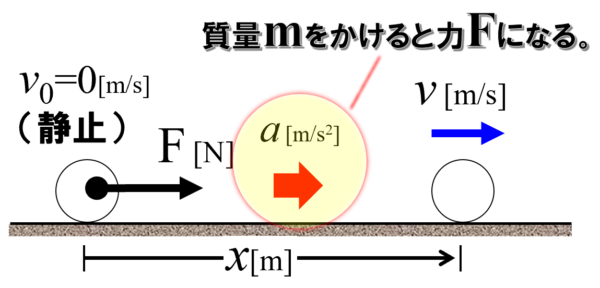
この力は一定です(加速度aが一定、)。

ということは、等加速度運動する時の物体を一定の力Fでxだけ移動かしたことになります。
ここで、もう一度等加速度運動の式に戻って、右辺を見てると、aがあります。これから、物体の運動と力の関係を考えるために、この式の両辺をm倍してみます。

運動方程式ma=F を考慮すると、右辺のmaの部分は物体にはたらいた力であると考えることができます。
したがって、右辺は2Fxとなります。

この時、Fxの部分が仕事を示すので両辺に2分の1を掛けます。
すると、こうなります。

最初、止まっていた物体が、速度vで動き出した。それは、物体に力Fが距離xはたらいたからである。

止まっていた物体が勝手に動き出すことはありません。
止まっていた物体に、力Fを距離xだけ作用させた。その結果、物体は運動能力を持つことが出来たわけです。

このようにして、運動エネルギーが定義されます。
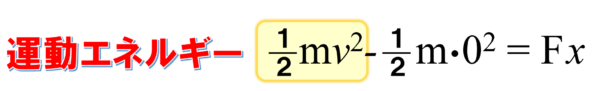
もう一度、この式の意味について言葉で整理しておくと、次のようになります。
力Fが距離xだけ働いたために1/2mv2の運動エネルギーを得た。
そして、この式を初速度v0を使って、一般的な形で表現すると次のようになります。
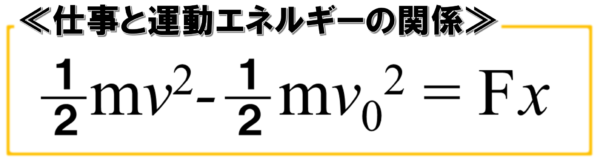
この式の左辺は、最初と最後の運動エネルギーの引き算になっているので、運動エネルギーの変化を示しています。

そして、力Fは、因果関係を示す運動方程式ma=Fから持ち出したFですので、この式にも因果関係が引き継がれます。
したがって、この式を言葉で解釈すると、「運動エネルギーの差は、仕事に等しい。」ではなく、「運動エネルギーの変化は、仕事によってもたらされた。」と解釈します。

運動エネルギーは勝手に増えたり減ったりしません。運動エネルギーが変化したという結果は、力Fを距離xの区間において作用させた、仕事という原因によってもたらされたものであるという因果関係があるわけです。
今回の解説は以上となります。次回の記事では、講義編の内容を使いながら実際の問題を解いていきます。














