目次
はじめに
それは教科書に載ってることだけど、もしかしたら…、

だから何なのこれ!?
って、思っている人がいると思うんです。

これがまさにコンデンサーなんです。
だから、実はコンデンサーって、簡単に作れるんです。
コンデンサーの充電と放電

ただ作っても面白くないですよねぇ…。
要は、金属版を2枚持ってきたらできます。

それは、ぜんぜん面白くないですよ。
だけど、これで、コンデンスすることができるんです。
コンデンサーの充電

そこで何をするか!?
電池につないでやるんです。


電池はポンプです。
ポンプでくみ上げる。

元々2つの鉄板は、電気を持ってません。
触ってもビッと来ない。

ところが、こういうポンプ(電池)につなぐと、ここ(負極側)にプラスとマイナスが同じ数だけあって、ポンプはプラスのものをガッと奪っていく。

例えば、具体的にプラスを2個奪ったとします。

そうすると、負極側の鉄板がマイナスなんだ。


プラスマイナスゼロのものからプラスを奪ったわけだ。
正極側の鉄板に移ると、プラスマイナスゼロのところに、プラスが来たわけです。

ならこうか!?

だから必ず相対する極板同士というのは、電気量の大きさは同じなんです。

プラスQとマイナスQ。

こういうのを充電したコンデンサーと言います。
最近はほとんど見かけなくなりましたが。ひと昔前にブラウン管型のテレビがありました。


あれは中で電子を飛ばして、正面の蛍光面にバ~ンとぶつけて、色とかを出してるんです。


電子は負の電荷ですから、プラスの方にグゥ~ンと引き寄せられてバ~ンと、画面にあたってるわけです。
そうやってテレビの画像を作り上げているんです。だから、ブラウン管型テレビの裏側を見るとほとんどの、そのテレビには、
サービスマン以外の方は開けないでください。
それはなぜかというと、危険だからです。

テレビ自体が危険なのではありません。
テレビの仕組みを知らない人が、ドライバー持ってきて中みてやろうと解体し始めると、それは危険です。

なぜかというと、コンデンサーというのは、
電源切っても電気が溜まっているんです。
プラスの電荷とマイナスの電荷は、クーロン力が互いに引き合っているけども、何かの拍子にガチャガチャいたずらをしてて、2つの極板を同時に触ってしまうようなことが起きると、その電荷が身体に流れ込んで来る。

だから危ないんです。
そういうことを分かってる人が開けるのであれば、何が危ないかがわかってるから良いですが、何が危ないかもわかってない人が開けると、感電でしてしまうしれないです。

だからサービスマン以外の方は開けないで下さい!
危ないですよ!
こういう風にして、コンデンサーというのは電荷を凝縮させておくことがでます。
コンデンサーの放電

そして、例えば蓄えたものに対して、次のようにしたらどうなるだろう??


こうやって電球付けて、スイッチつけて。
スイッチをぱっと閉じると、どうなるか?

電気がグルっと回るから、そのときにピカッと光る。
その代わりに、電池みたいにず~っと持ち上げる装置があるわけじゃなので、一瞬ピカッと光っておしまいです。

一瞬ピカッと光る…

さて私は、今何の話をしたんでしょうか?
もちろんコンデンサーの話です。
何かピカッと光るもの。

わかったでしょ!?

カメラのフラッシュです。
例えば、携帯電話にカメラがついてます。中に電池が入ってますが、

大体あんな小さな電池で、なんで一瞬だけ明るい電気がつくのか!?

例えば大きな単一の乾電池使っても豆電球がボワ~ンと光るぐらいです。

だけど、コンデンサーだとめちゃくちゃ明るいのが一瞬だけ光ります。

何をしたの!?

一カ所だけ、ちょっと凝縮させてあるんです。
カメラのスイッチをパッと押した瞬間に、その凝縮してたものをバァっと一気に流し込んだんです。

カメラのフラッシュは一瞬でいいから、コンデンスしたものを一気にバァーっと放出させて、弱い電池でも強い光を生み出すということができるわけです。
小さな電池では、ちょろちょろちょろちょろとしか電気は流れません。
だから、ちょっとしか明かりがつかない。
そこで何をするかというと、いったんそれをバケツに汲むんです。
ちょろちょろとしか出ないけど、バケツに目一杯溜めましょう。
そして、シャッターを押した瞬間にそのバケツをひっくり返しましょう。
そしたらドォ~ンと、一気に流れますから。

これが電池とコンデンサの違いです。
コンデンサーは明かりを付けることが出来ますが、電池は長時間つけることができるのに対して、コンデンサーは一瞬しかつけることができません。

そういう違いを、まずは分かってください。
コンデンサーに蓄えられた電気量
そして、もう一つ。プラスQとマイナスQが蓄えられた状態になってる時に、この2つの電荷は引き合ってると言いました。

ということは、これを放っておくと重力とか関係なしにペタンってくっつくんですねぇ…
プラスQとマイナスQがくっつきますから、やっぱりゼロになります。決して生み出されたわけじゃないんです。移動しただけなんです。だから、ペタンとくっついてしまえば、もともとのゼロになってしまうということなんです。

そんなに難しい話じゃないですねぇ。
そして、例えば回路があって、ここにQクーロン、ここにマイナスQ、必ず相対するものの電気は大きさは同じです。ここもプラスQにしておきます。そして、マイナスQ。こうなってます。
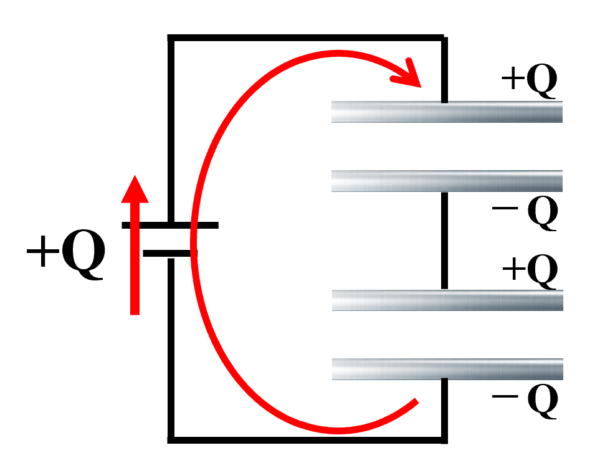

全体としてどれだけの電気量が蓄えられてるでしょう?
ただし、一応言っておきます。次の図のようになることをQ蓄えているといいます。
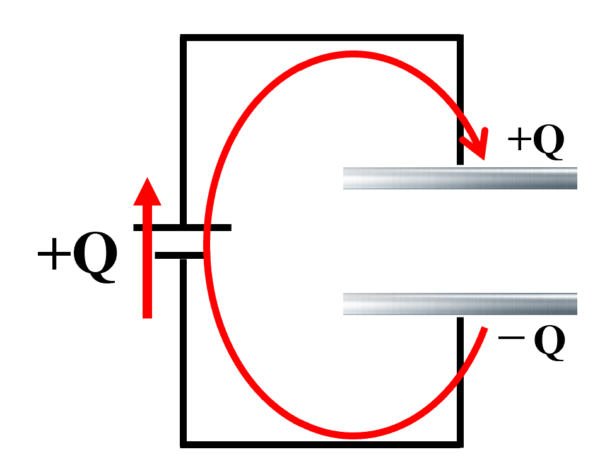

では全体としてどれだけ蓄えられているでしょう?
もう分かりましたか…??

私がクイズにしたということは、答えは2Qじゃない!
ということです。

なんで、そんな裏から考えるんだ!?
って言われるかもしれませんが、

ここがQでこれがQであわせて2Qだ!
っていうのは、クイズにならないですよね。
どれだけ蓄えられているか…??

答えはQです。
大丈夫でしたか??
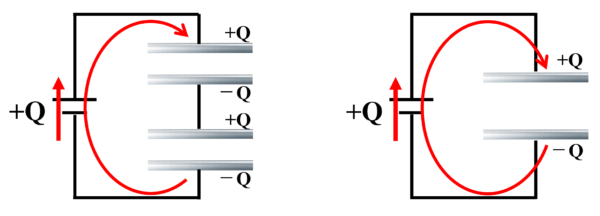
左の状態も右の状態もQだけ蓄えられてる。

その辺りが分かるかどうかなんです。
左の回路のカタカナのエっていう字、その金属に注目してください。

これは一つの金属です。合わせたらゼロになります。

なぁ~んだ、ここは何も蓄えてないんだぁ…。

じゃあ、ないのと一緒じゃん。
コンデンサーにした仕事
続けていきます。ある時に一番最初は何にも蓄えてないゼロの状態から、片や図①のようになった。片や図②のようになった。


ところで、電池はポンプなんですよねぇ…。
ポンプっていうのは、電荷を上に上げるという仕事をしているはずです。

じゃあ、①と②のした仕事。
どっちの電池が大きな仕事をしましたか?

正解は、どっちも同じです。

①の図は、プラスQが2つにマイナスQが2つ。だったらこっちの方がいっぱい仕事したのでしょう!
って言っちゃいけません。
よく考えてください。

電池っていうのは、持ち上げること。
ということは下の極板から、電荷を持ってきて、よっこいしょって、上の極板まで持ってきたはずです。

ここ(青の点線)の空間は飛べません。

下の極板から上の極板を移動した電気量って、プラスQクーロンを持ち上げたんですか?
下の極板は、プラスQを奪われるからマイナスQになる。上の極板はQがやってきたからプラスQになったんです。

では、②の回路は?


もともとゼロゼロだったんですよ!
奪って持ちあげた。そうしたらプラスQ。

何だぁ!持ち上げたりも一緒なんだぁ。

それじゃあ、もしも電圧が等しかったらどうか…??
同じですよね。

要は、こういうふうに、どれだけの物を持ち上げたか!?
というような事を、考えること。

W=QVとか。変な式をたくさん覚える人がいるけども。それを覚えちゃいけないとは言いません。

しかし、なぜそういう式なのか!?
ということが分からないと意味がありません。

(電池は)位置エネルギー与える装置であり、1クーロンあたりVだけの仕事をするわけです。それならQクーロンでは、QVだけの仕事をするんです。
それで①の回路も②の回路もQVだけの仕事をした。それは、同じじゃないかと言ってるんです。
今、まるでね雑談のように喋ってきましたが、

今のは単なる雑談ではない!
っていうことは分かってもらえるでしょう。
その定性的な部分でも定量的な部分でもそうですが、

電荷の動きは、私たちの目には見えません。
もっと極端なことを言うと、本当は負の電荷が動いてるんです。

そういうのを聞いたことがありますよねぇ…。

電子が見つかったいうのは、1905年なんです。
1905年って言ったら「発表された時」と言ったほうがいいかもしれないので、1897年と言った方がいいのかもしれません。

イギリスのJJトムソンという人が、電子を発見しました。
それで、みんながあーだこーだと議論しながら、1900年の頭ぐらいに、
それで良さそうだ!

今から120年ぐらい前です。
コンデンサーはボルタという人が一番最初に作ったので、もっと前の話です。
だから、

厳密には、本当は電子が動いてるはずだ!
っていう、そういう考え方が必要な時もありますが、特定の回路の問題を考える時には、プラスのものが動いているということで構いません。

随分話が長くなりましたが、今のような定性的なことと定量的なことを分かっていなければいけません。
コンデンサーの極板間力

この引力は、一体どのぐらいだろう??
っていう訳です。

点電荷同士でプラスQとマイナスQという風になれば、この力を知ってるでしょう!?

ということは分かってる。


引き合うということは、どうも分かりますが、どのくらいの力があるか…??

どうやって計算したいいの??

ここでは、こうやって考えるんです。
上の方にあるプラスQクーロンの平行板コンデンサーから、電場が発生している。
電気力線は全部で4πkQ本だから、上に2πkQ本。下に2πkQ本。
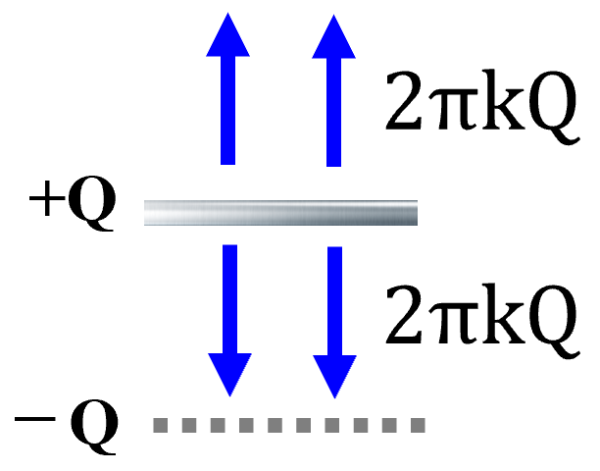
この2πkQということは、4πkQの半分ですから、ここの電場は2分のE。

もちろんEというのは、コンデンサーの電場の大きさです。

この中に、マイナスQクーロンの電荷を入れると、どうなるか??
と考えるんです。

それがマイナスですから、上に引っ張られるんです。
そのとき受ける力は、2分のEの中にQを入れたわけです。
そうすると、コンデンサーの極板間力の大きさFは、次のように表現できます。

Fは大きさです。なので、ここに絶対値の記号をつけておきます。すなわち極板間力Fの大きさは、2分1のQEと書けました。

これも大事な式です。
このF=2分の1QEという式を、ただ単に覚えるっていうのは反対です。
普通に考えると、

F=QEじゃないの!?
って言いそうなのですが…

でも違うんです。
公式として覚えてしまうんだったら、2分の1QEなんだろうけども、

この2分の1っていうのはどこから出てきたのか??

4πkQの半分の2πkQ!!
そこから出てるんだっていうことが、ちゃんと分かっていないと、式を覚えても意味がありません。
そうやって、極板間が引き合う力というのが分かりました。
だから、この極板の力に合わせてというか、釣り合うように何かこう維持しておくものがないと、

コンデンサーの極板がグぅ~っと縮んでしまう…
ということになってしまう。
(金属板に働く)外力がした仕事について
それで次に2枚のコンデンサーをひっぱって、dだけ動かした場合を考えると、
その時の仕事は、極板間力2分の1QEに逆らってdだけ動かしたわけだから
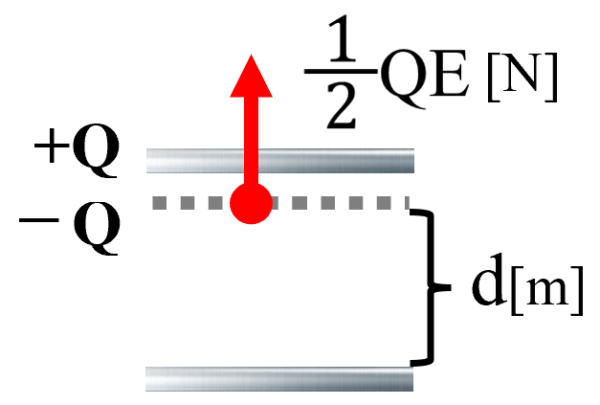


これがコンデンサーにした仕事になるわけだけど、コンデンサーに仕事をすることによって、コンデンサーは能力を持ったことになります。
これをコンデンサーの静電エネルギーと言ったりもします。


それでは最後になりますが、テレビのようなものは分解すると危ないですが、もしかしたら、ラジオとかのを中を見たことある人がいるかもしれません。

それからもう一つはセラミックコンデンサー。茶色くて2本の足がぴゅっと出た茶色いやつです。

ああいうものが、コンデンサーと呼ばれています。
そういうものの中に電荷を蓄えることによって、何かをしてるんですね。勿論いつもカメラのフラッシュみたいなものばかりではありません。もっともっと用途は大きいです。

そういうものを直に目で見てみるということも大切なことだと思います。
そして今回やったような定量的なこと、定性的なこと。そういうことをつかむということも大事です。
■コンデンサーの問題演習1(制作中)

















