円運動の加速度
円運動の速さと加速度

まず少し加速度の概念を使いながら、お話をしていきます。
等速円運動している時に、物体があって、v という速さだったとします。
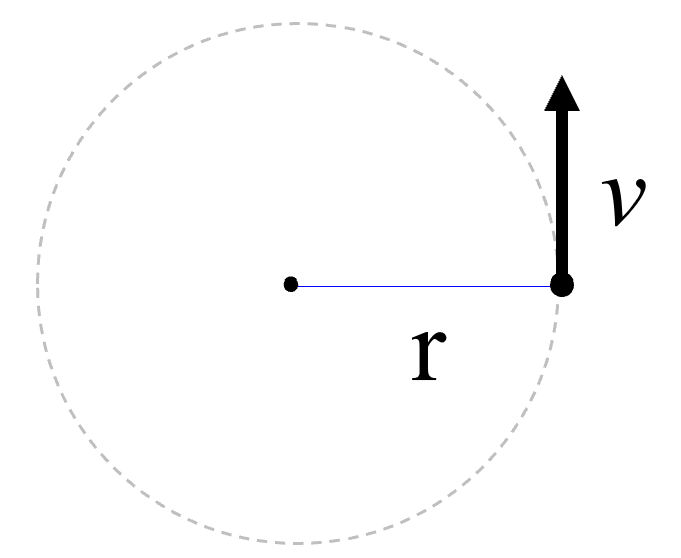
グルグル回っていくわけですね。1秒後にこういう風になったとします。

ということは、1秒後ですから、回転した角度は ω に等しいはずです。
それで、今v が、図のように変わったんです。
(加速度の定義から)単位時間当たりの速度変化が、加速度になるわけです。
ですから、

ベクトルっていうのは、平行移動しても構わないわけですから、矢印の根元をくっつけてしまいます。
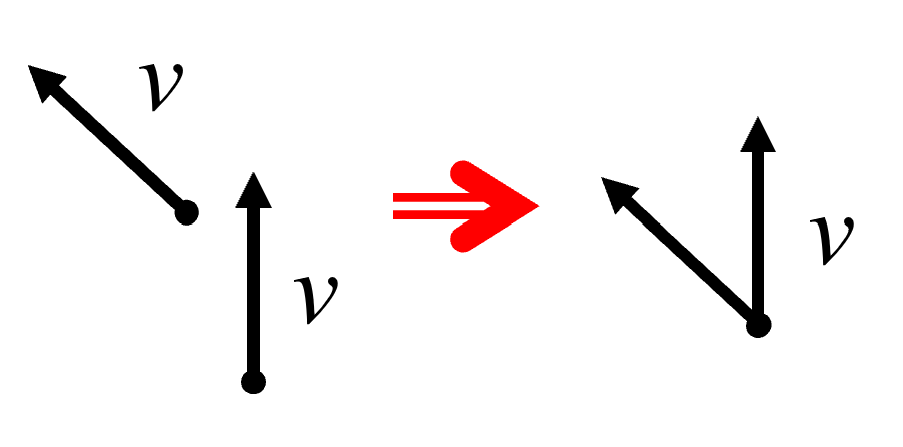
そうすると、次の図の赤い線だけ変わったことになります。


変わった量ですから、これが加速度です。
この時、角度がω だけ変わったから、2つのベクトルがなす角度はω ですね。
ですから、



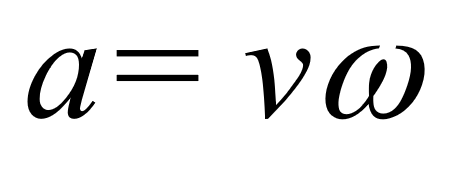
それで今、この物体は回っています。

円運動の速さの式です。




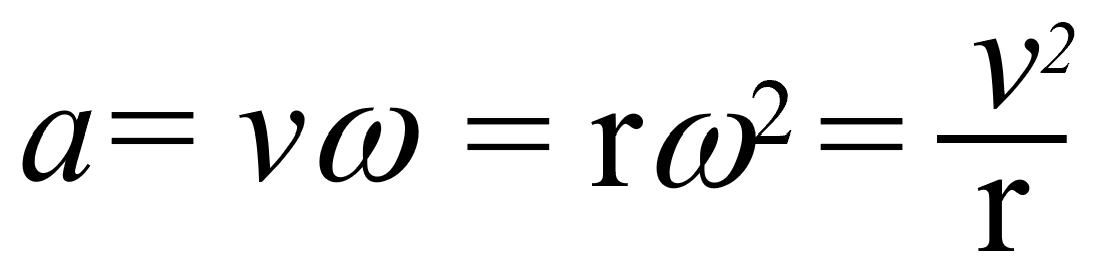

円運動の加速度は、いろんな表記を持っています。
加速度の式が持つ意味とは!?
皆さん。ここからがとても大事です。

この加速度の意味はなんですか??
それでは進めていきましょう。

それは記号を覚えているだけです。例えば a = r / v2 2乗、 a = rω2 の2乗。これをとりあえず覚えているだけ…。
確かに問題を解く時には、この2つの式はとてもよく使います。
しかし、どのような意味を持つ式なのかがわからないと、

ということになってしまいますから、

今から、少し話を聴いてください。まずは、先ほどの話を思い起こしてください。
月は地球に向かって落ち続けているんです。


ニュートンの弟子たちが書いた伝記で、本当かどうかはわかりませんが、こういう言い伝えが残っています。
ニュートンは、


って、
ずっと考えていたんです。しかし、いつまで経ってもわからない。


すごい自信ですねぇ。
要は、

実は、アリストテレスが言ったように、地上界と天上界、別々の運動だよって言ってるけども、

と。
だから、

こう考えたんです。

そして、今、ここで幾何的に求めた加速度の式と一致することを示したんです。
そうすることによって、

ということに気付いたんです。
ニュートンは、学会で多くの物理学者を前に、こう言いました。


それに対して、周りの科学者たちは、

と、
普通は、そのように言い返すでしょう。
しかし、

ニュートンが、

と言った時に、

月は落ちてるんだ。
と、考えられるようになってください。
何も難しいことを言おうとしてるわけじゃありません。

それでは、こんな風に考えてみます。
まず、ここに地球があるとします。

それから、その真上にしましょうか。ここに月があるとしましょう。
![]()
小学校の頃に、天体の話を教わって、月が地球の周りをくるくる回っているという事はご存知だと思います。
しかし、その前に、

月は、あっという間にどっかに行ってしまいます。

そらそうです。

月は静止しているわけじゃなくて何らか速度を持ってるので、地球が引っ張らなかったら、そのままスゥ~っとはるか遠方に飛び去ってしまいます。


回っているんです。
そうすると…、ある時は、ここです。
![]()
そして、ある時、お月様はここにいるんです。
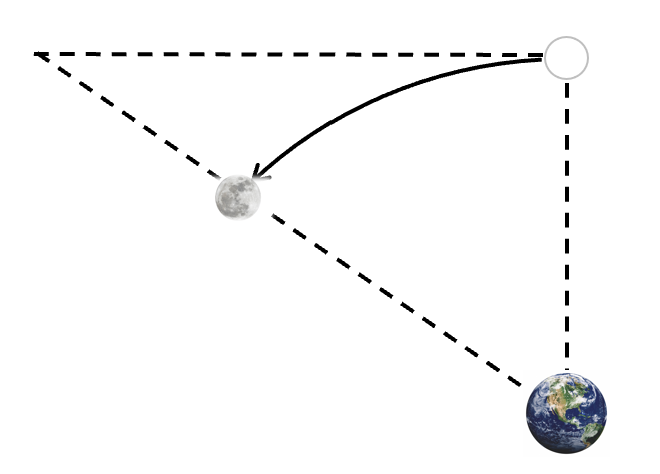
この距離、地球に向かって落ちてきたんですよ。
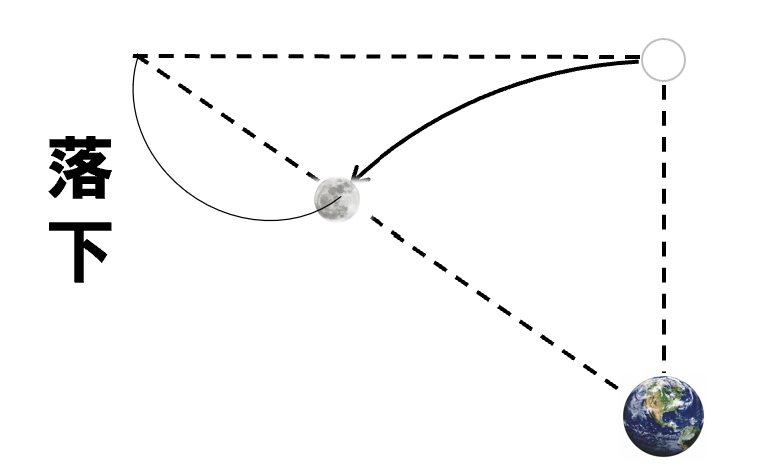
もし何も力が働かなければ、月は、ここにいたはずです。
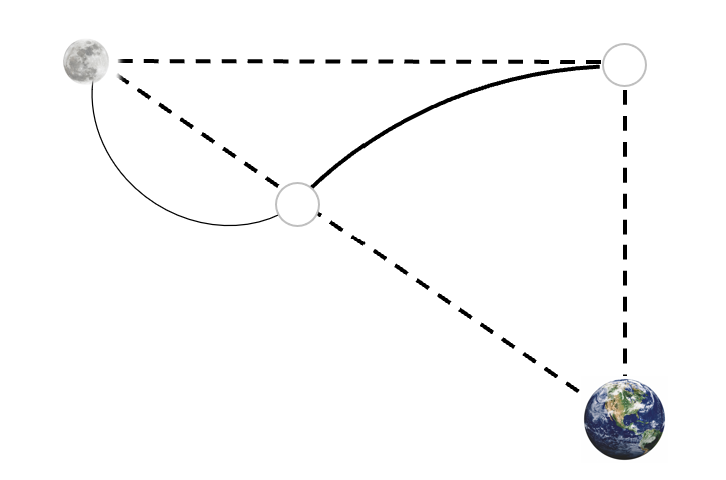

りんごが落ちるように…。
りんごをここで手を離したら落ちてきます。

それと同じように、これだけ落ちたんだという考え方をしたんです。
要は、

こう考えたんです。
そして、ニュートンが何をやったかって言うと、月は軌道半径をr 、速さv で動いてるとします。
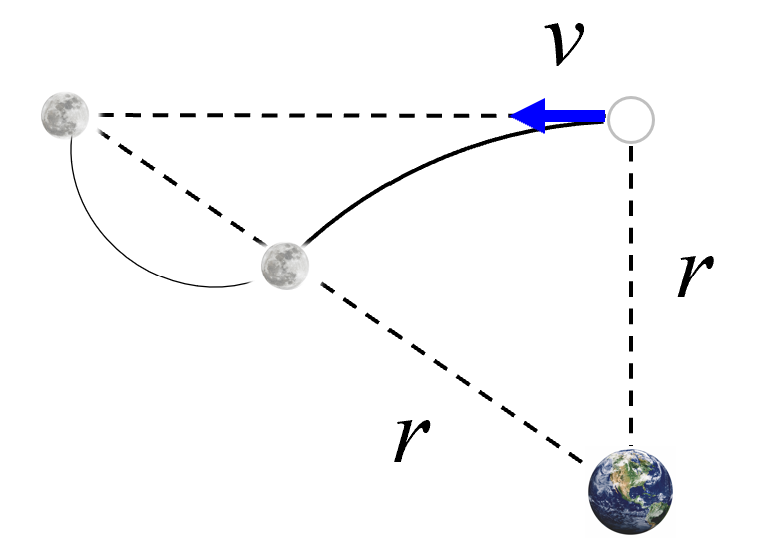
そうすると、一定の速さでまっすぐ進むから、この距離をvtと置いたわけです。
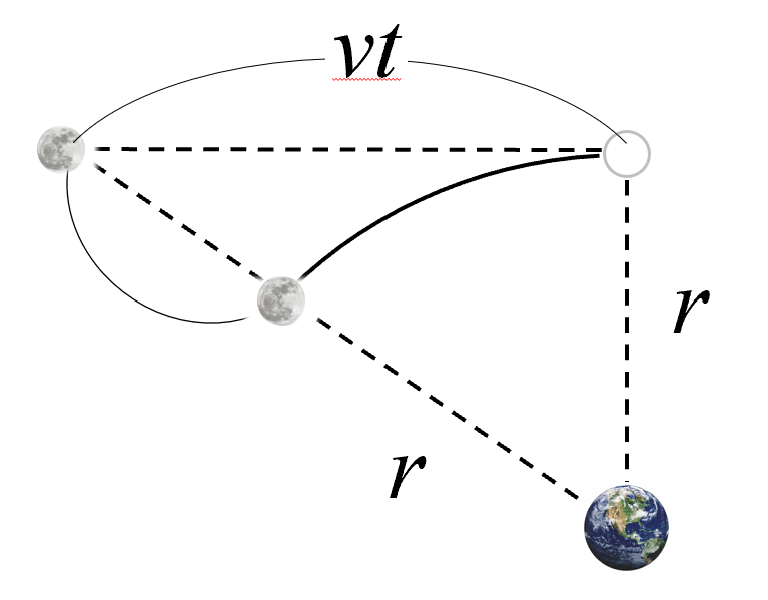
その時に、こういう方向に落下したと。加速度はa とします。
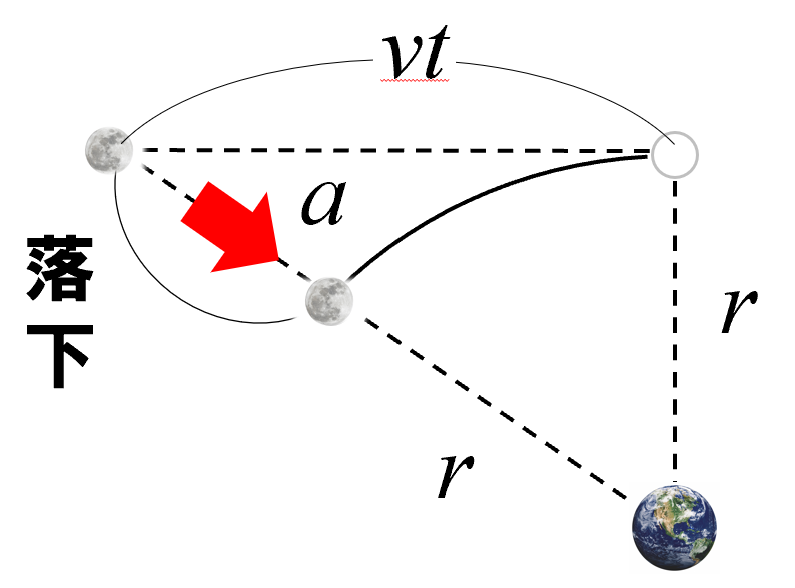
加速度a で t 秒間落下したと考えた。だから、等加速度運動の式に近似したんですねぇ。
1/2 at2だけ落下したんではないかと。
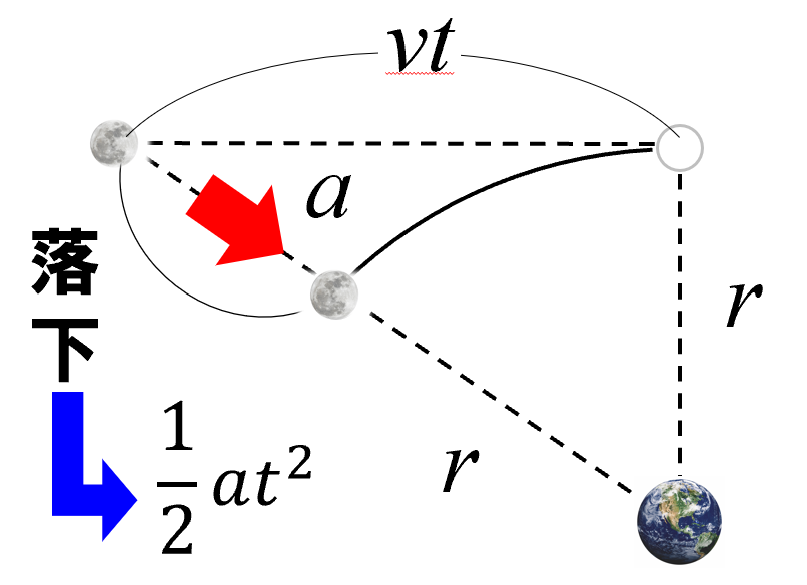

それに対して、ここが直角三角形になります。

そこで、三平方の定理をニュートンは使っていったんです。やってみましょう。
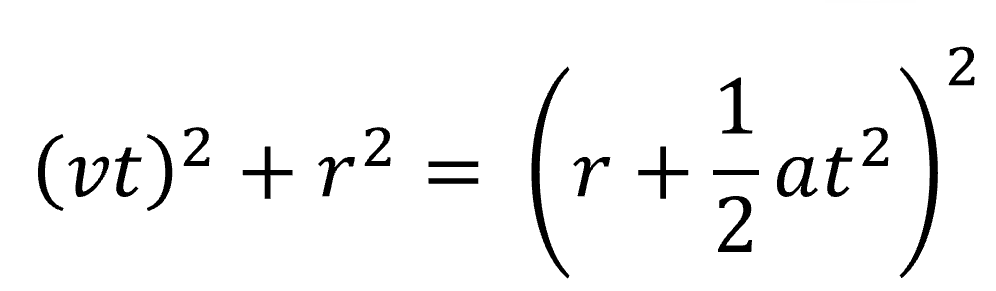
すると、底辺の2乗足す高さの2乗が vt2 + r2 です。一方、斜辺の2乗が、(r+1/2at2)2となります。
それでは展開しましょう。
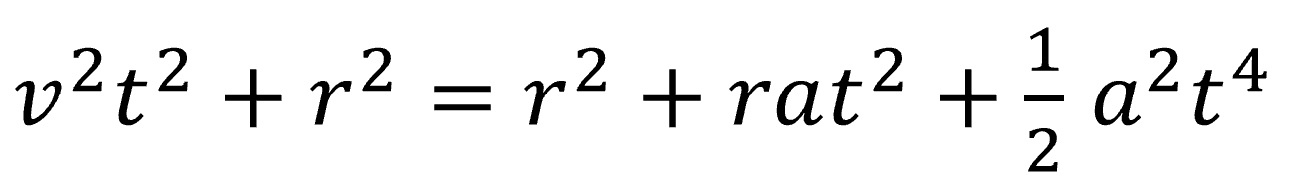
こうなります。では、続けて行きます。
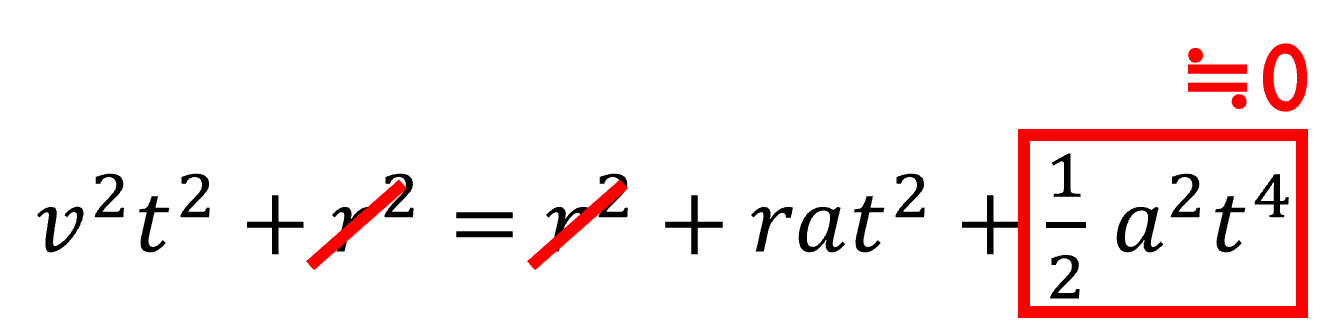
ニュートンは、1/2a2t4を≒0と置いた。

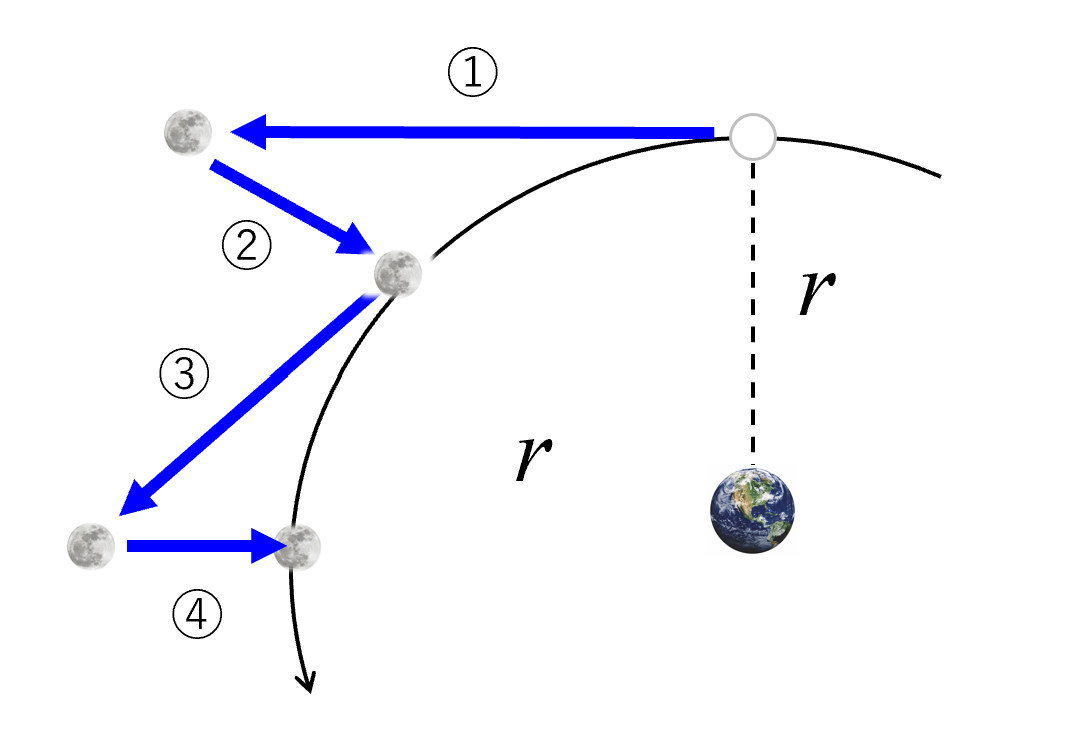
月は、図の①➝②➝③➝④のように、こういって、ど~んと落ちて、こういって、ど~んと落ちているわけではありません。

だから、この三角形は微小なわけです。
ですから、1/2at2は超微少量なんです。それを2乗したのが 1/2a2t4です。

ですから、この 1/2a2t4 をゼロに持って行ったわけです。

実際には、こうした三角形上に落ちてるわけじゃないですからね。
そうすると、残ったのは、
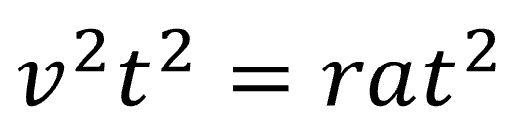
そうすると、t2 はゼロではないですから、約分すると、


先ほど、ベクトルを使って幾何的に求めたやつです。
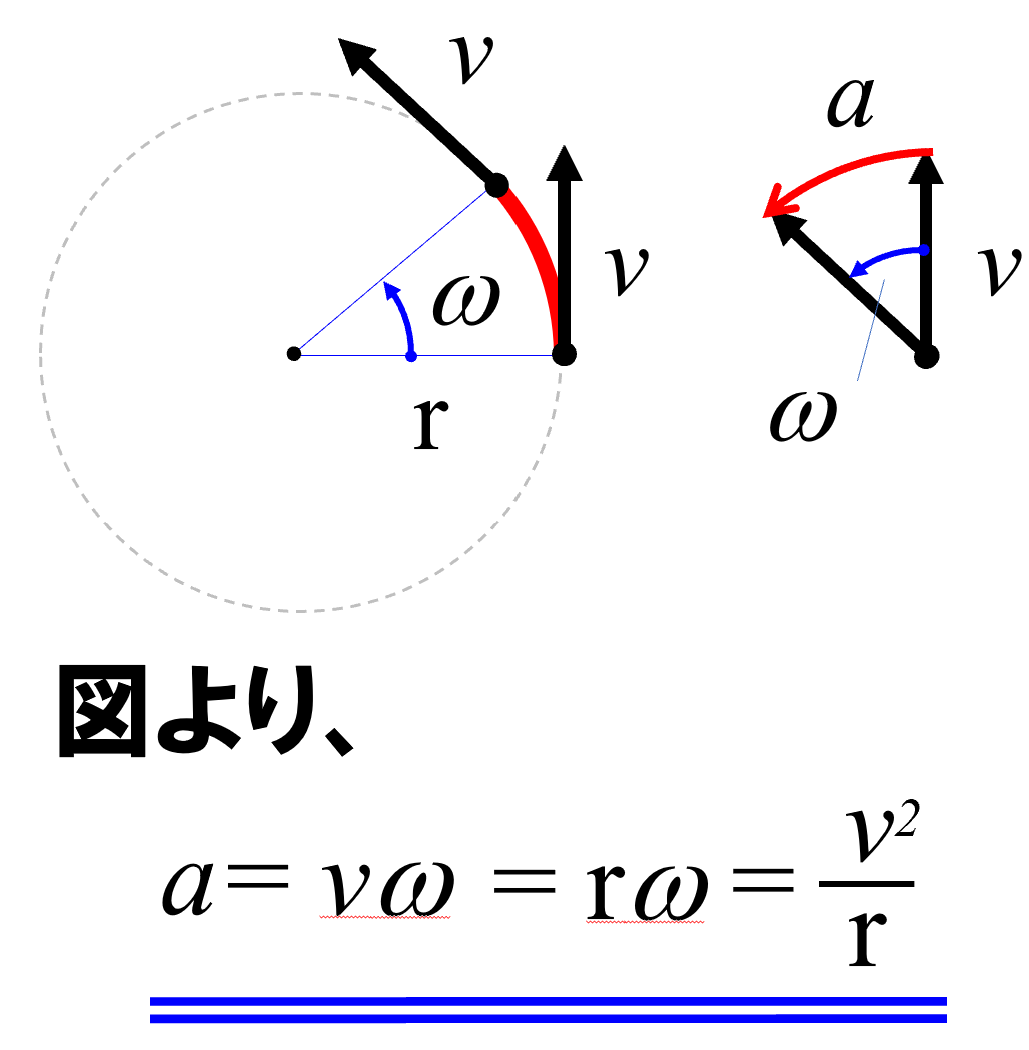
幾何学な導出だと、v = rw をこう代入していって変形しただけです。それだと、とても意味がわかりにくいんです。これは…。
ところが、今みたいに、

という考え方をしながら、こちらの考えを使うと、意味がとてもよくわかりますねぇ、
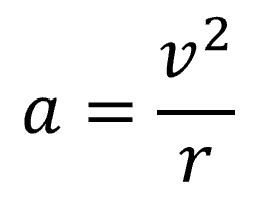
この加速度って、月が地球に落ち込むっていう意味でしたね。
これに質量かけたら力と同じですから、

円運動っていうのは、円の中心方向に落ち込む現象。
これを扱っているんですねぇ。

あれ、落ちてるんですよ。地球の中心に向かって…
こうやって、落ち込むという現象なんだということは、わかってもらえたかと思いますから、少しまとめてみます。
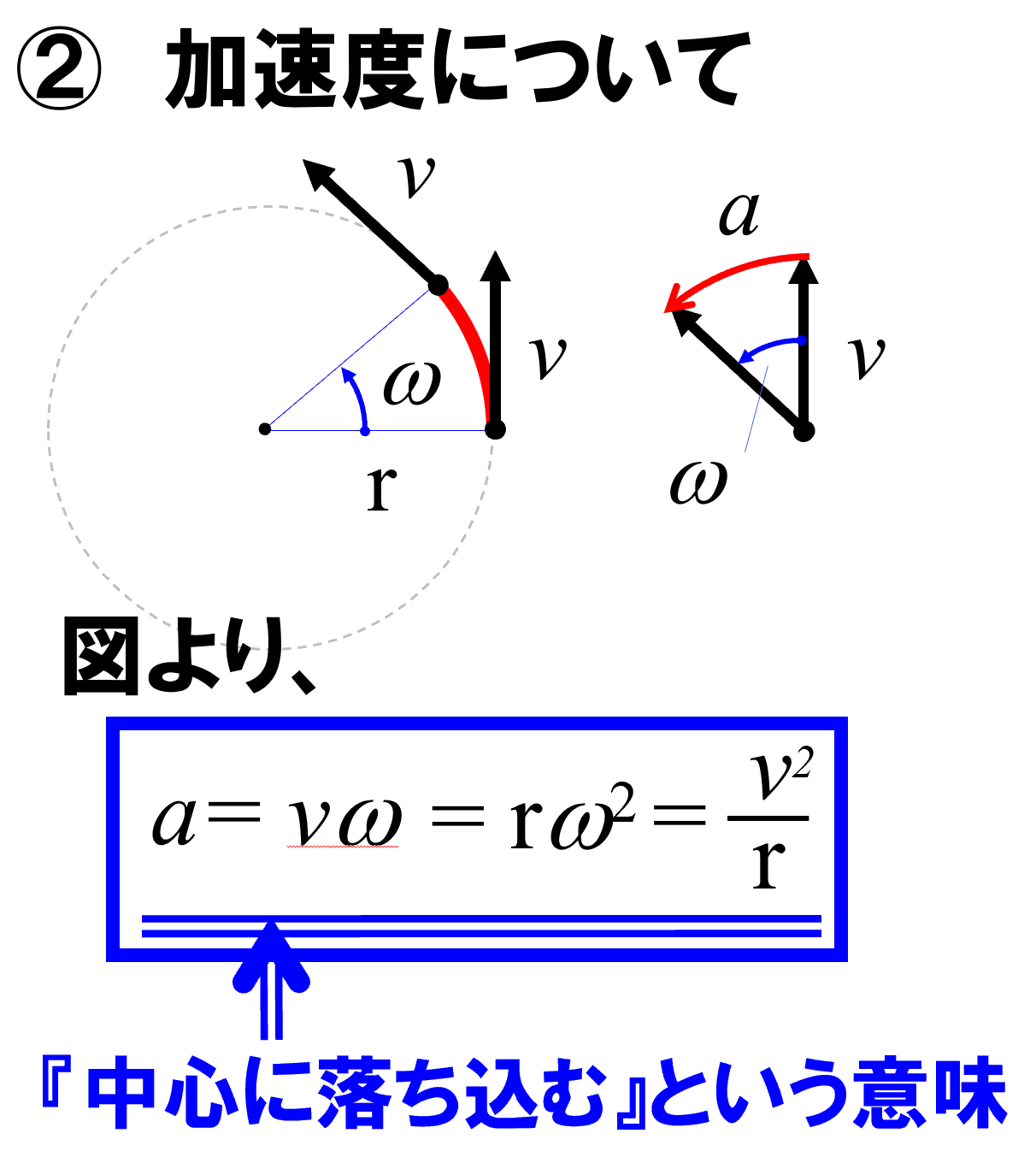
「地球の中心に落ち込む!」ということ

ニュートンがそれを発表した時に、多くの、科学者たちは、

落ちてこないではないか!?
と誰も納得しなかった訳です。
そこでニュートンは、こんな説明をしました。
ここに地球がある。

この地球に、ものすごい高い山を用意するとします。
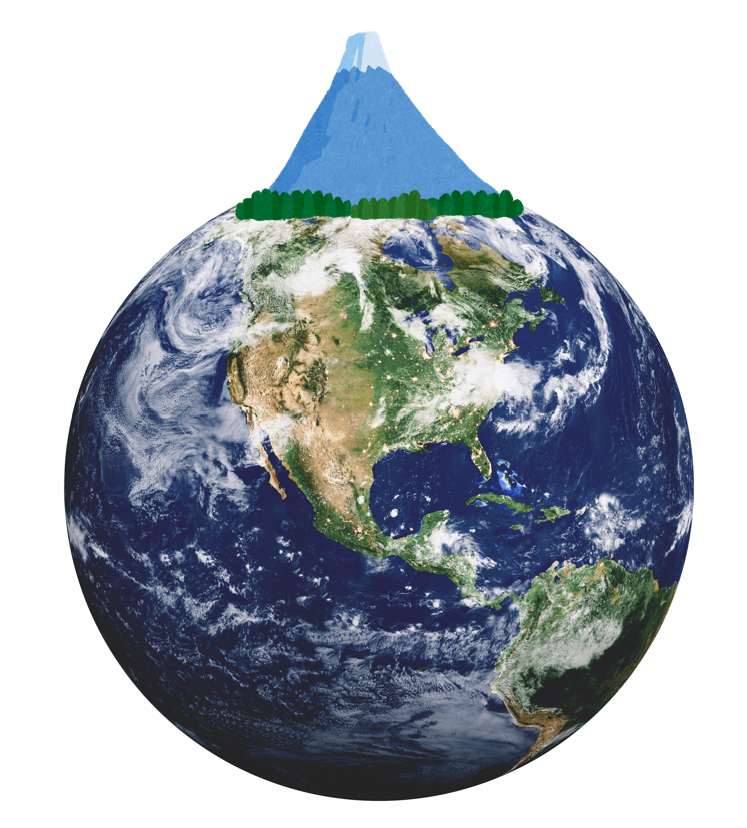
そして、そこからボールを、水平方向に投げてください。
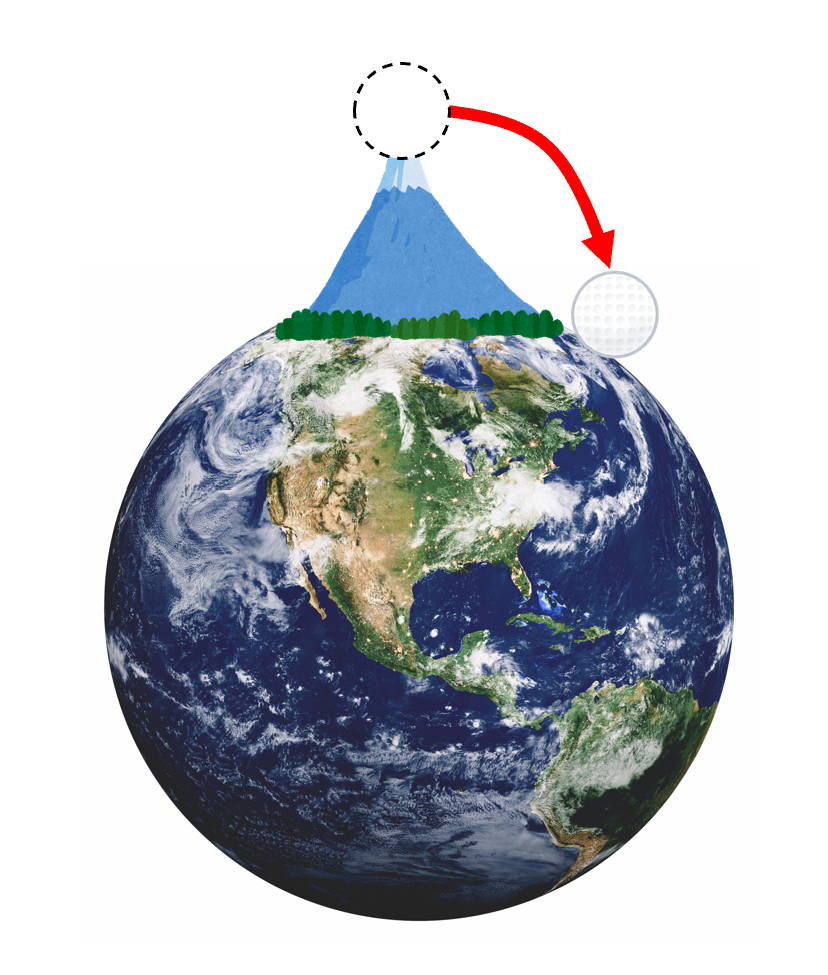
そうすると、「ぴゅ~ん」と飛んで落ちます。

もうちょっと勢いよく投げてみます。
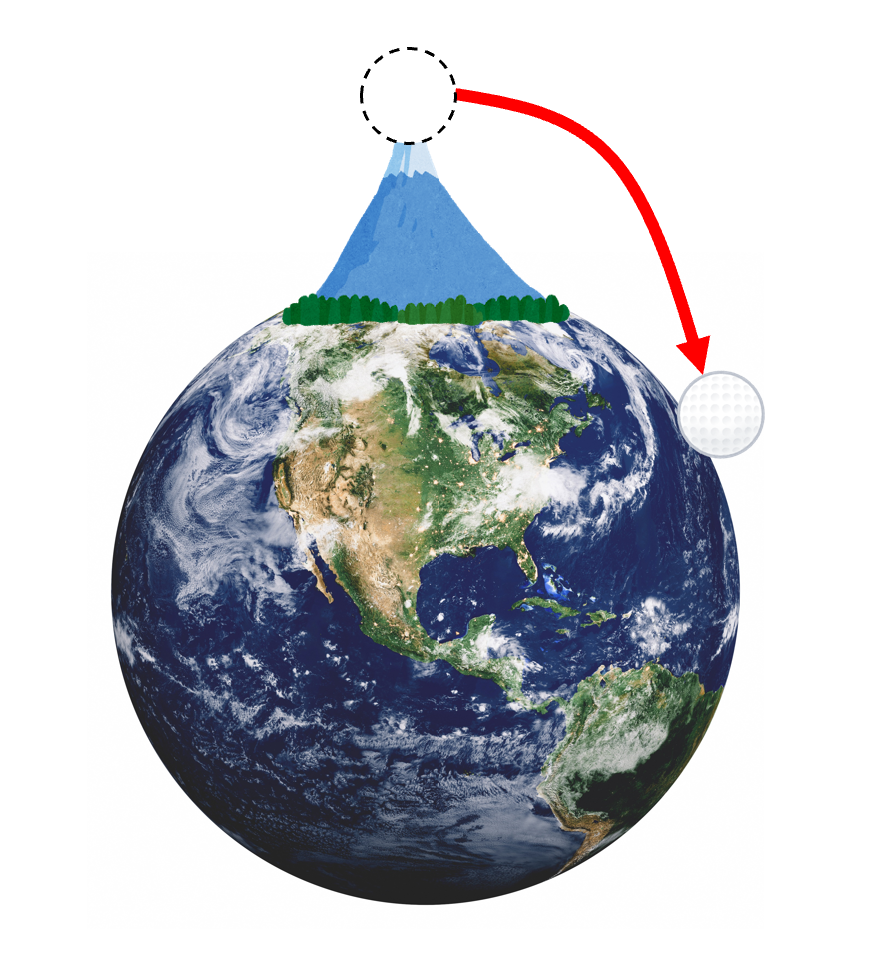
そうすると、もうちょっと遠くに届きます。

それでは、もうちょっと上手いこと投げてみましょう。
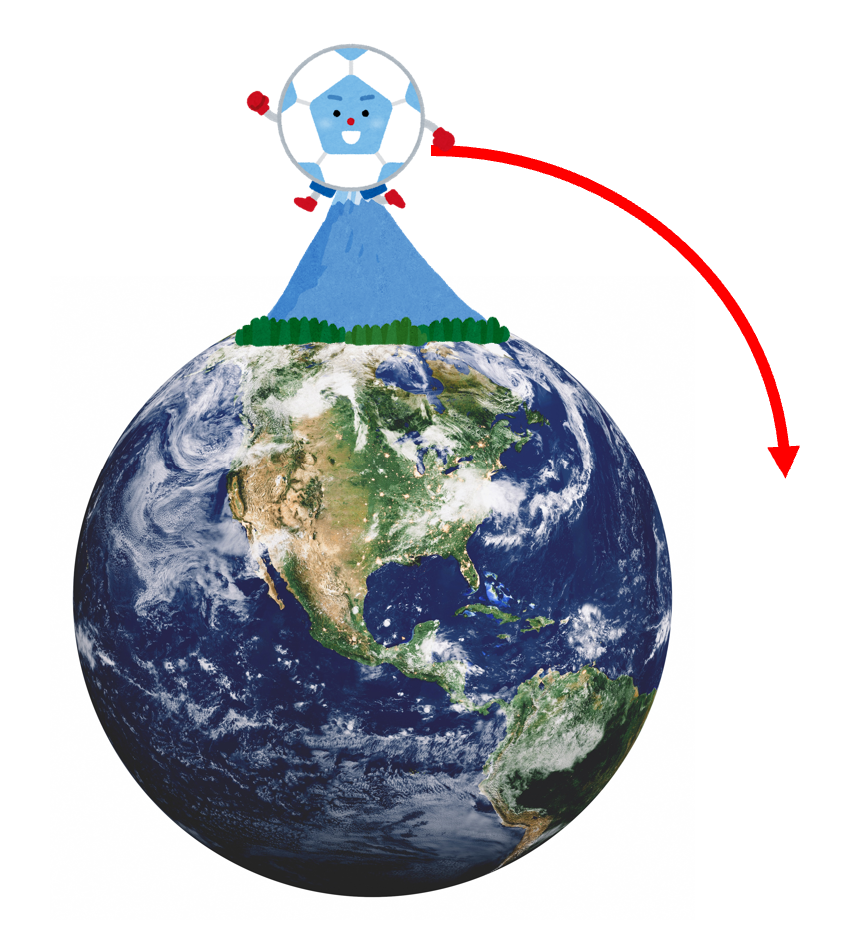
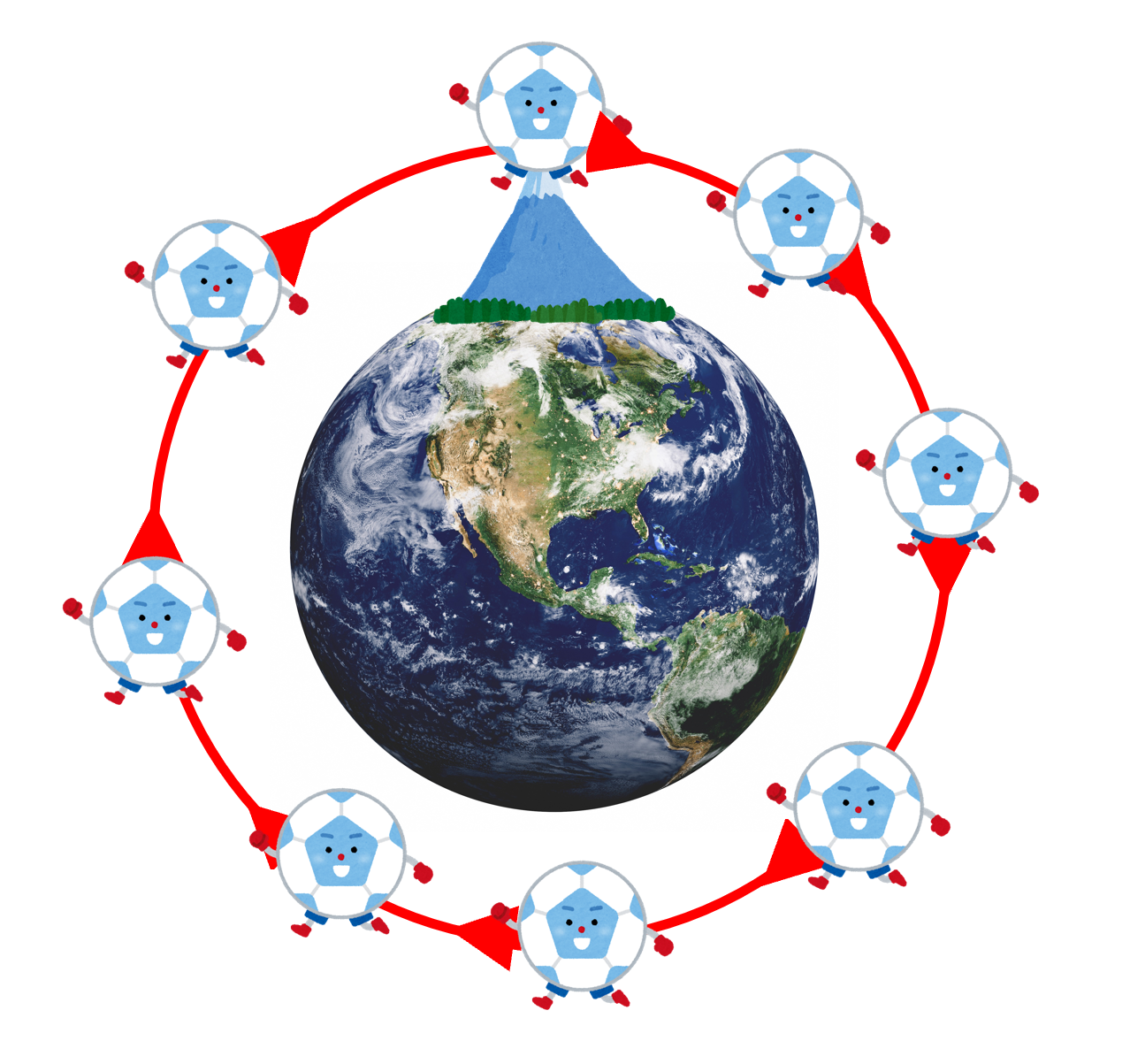
これが「落ち続ける!」ということです。

だから、人工衛星を打ち上げる時には、ど~んって打ち上げて、

ある高さまで来たら第2段ロケットでびゅ~んって打ち出すんですね。
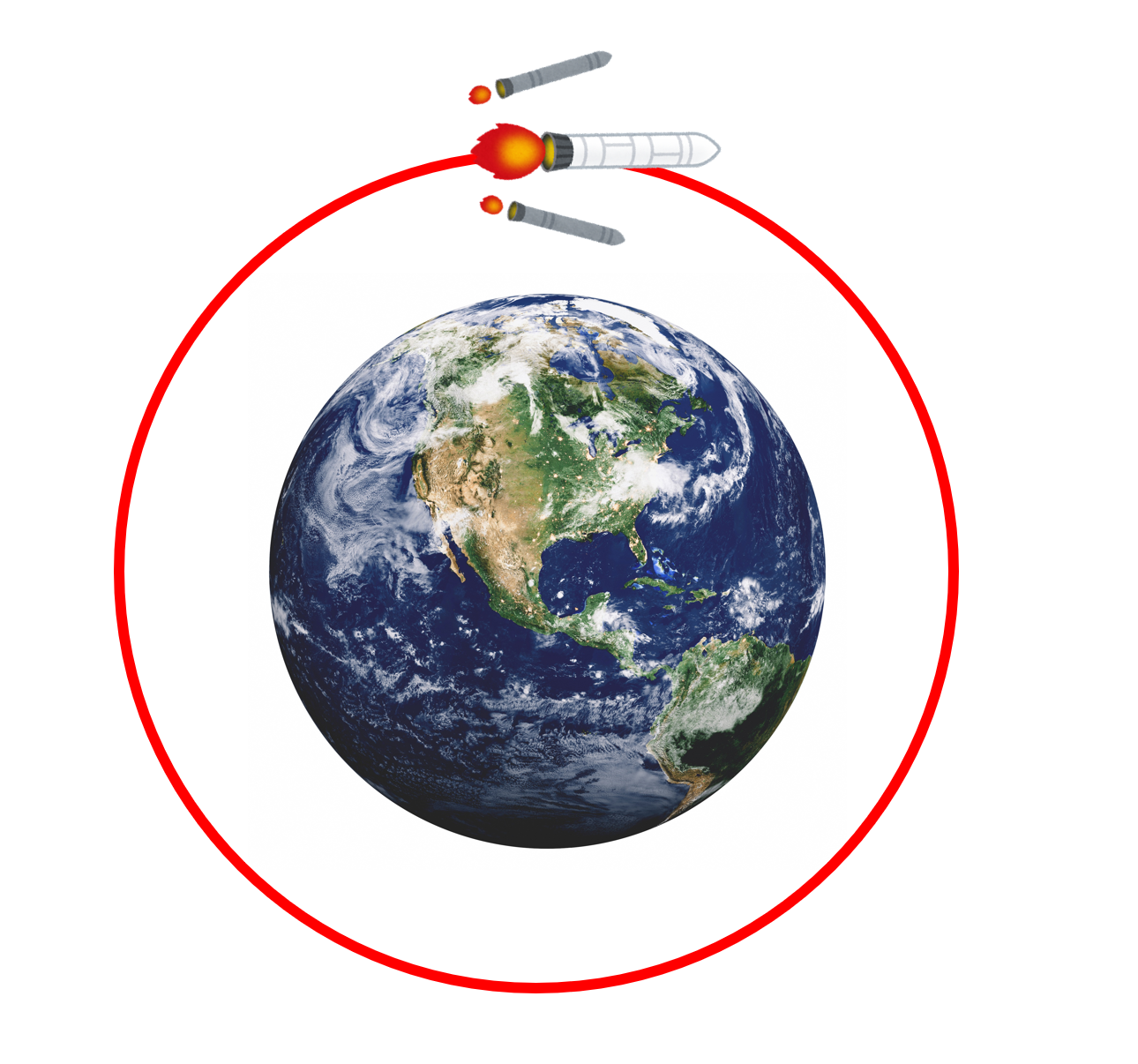
そうしたら、後は延々と回っていられるんです。燃料が要らないんですよ。
もちろん太陽電池とか一杯積んでいます。しかし、それは中のコンピュータを動かすためです。
グルグルまわるという事に関しては、何のエネルギーも使いません。

1600年代にこういうことはわかっていたんです。
しかし人類が、人工衛星の打ち上げに成功したのは、1900年代に入ってからです。
300年以上もかかっています。しかし、その人工衛星のお陰で僕たちは、地球の裏側とでも交信が出来るようになりました。
静止衛星のお陰で、地球を遠くから見て、明日雨が降るかどうかを雲の様子とかを全部撮影することで確認出来るようになりました。
しかし、それらは回るという事に関しては、何のエネルギーも使っていない。

地球自体は何のエネルギーも使っていません。だから、地球は太陽に落ち続けているんです。
しかし、

これをしっかりと理解してください。

それは、

っていうことになります。